
The Complexity Dynamics
of Magic Cubes and Twisty Puzzles
6th Jan
2020 PDF website http://dhushara.com/cubes/
Fig
1: A selection of the twisty puzzles discussed in the article: (1-9) show wide
variation in cubic rotational geometries. (10-17) show how the geometry of the
external shape affects the puzzles. (18-20) cube variations and (21) show a stickerless 9x9 cube to explore how increasing sizes of NxN puzzles affect the solutions. (1) A 4x4 Rubik cube. (2)
MF8 face and corner turning windows grilles cube. (3) A Moyu 4x4 axis 4x4 cube shape mod. (4) MF8 crazy unicorn cube. (5) MF8 4-layer elite
half-cube turning skewb. (6) A 45o turning
MF8 sun cube. (7) A 45o slice-turning MF8 Son-Mum V2 4x4 cube with
additional splits to enable additional confirmations (8) A Dayan Shuang Fei Yan (cool flying
swallow) corner and oblique turning cube. (9) MF8 edge-turning ‘twins’ Skewby Copter plus. (10) Alexander’s Star great
dodecahedron. (11) Shengshou Megaminx dodecahedron. (12) MF8 multidodecahedron containing a megaminx inside a master penultimate (13) Jiehui rhombic dodecahedron. (14) Qiyi Qiming pyraminx corner/face
turning tetrahedron. (15) Stickerless Shengshou mastermorphix edge-turning tetrahedron 3x3 cube shape mod. (16) LanLan face-turning octahedron. (14) LanLan 4x4 corner
turning octadedron. . (18)
Square-1. (19) Fang Cun Ghost Cube 3x3 shape mod.
(20) Mirror Cube 3x3 shape mod. (21) MoYu free-turning stickerless 9x9 speed cube.
History:
In the
mid-1970s, Erno Rubik designed his 3x3x3 "Magic
cube" (Buvös kocka in
Hungarian) as a way of solving the structural problem of rotating the parts
independently without the entire mechanism falling apart. He did not realise
that he had created a puzzle until the first time he scrambled his new cube and
then tried to restore it. The Pyraminx was made and
patented by Uwe MŹffert in 1981. The original Skewb is a shape modification of a Pyraminx
invented by Tony Durham and marketed by MŹffert.
Robert Webb designed the corner-turning Dino Cube in 1985. The original
prototype was made entirely out of paper and first marketed with images of
dinosaurs on the faces. The master and elite versions (8) now have distinct
additional transformations distinct from an nxn
pyraminx. The Megaminx
dodecahedron, or Hungarian Supernova was invented in 1982 by Ferenc Szlivka. In the same year,
a slightly different design was made by German mathematician Christoph Bandelow and produced by MŹffert.
Alexander's Star was invented by US mathematician Adam Alexander in 1982. It
contains only edges in 6 colour pairs for the 12 faces and is equivalent to
solving only the edges of a six-color Megaminx. The Square-1 layered shape-shifting puzzle with
non-cubic scrambling was invented by Karel Hrsel and Vojtech Kopsky around 1990. The
edge-turning Helicopter Cube was invented by Adam G. Cowan in 2005 and the
curvy, plus and skewb versions by Tom van der Zanden.

Fig 2: Four core cube
designs and their rotations: The 2x2 face-turning Rubik Pocket cube, the slant-turning
Skewb, the corner-turning Dino cube and the edge-turning Helicopter cube.
Puzzles
2, 4 and 8 all contain similar corner-turning moves to the Dino cube, in
addition to other move types. The Dino Cube is one of the easiest puzzles to
solve since: (a) Each move only affects a small corner
collection, so it is easy to solve one part of the puzzle without disturbing
what is already solved. (b) Each piece only has one possible orientation, so if
it is in the correct position, it correctly oriented. These features also
appear in the composite cubes.
With the advent of computer programmed 3D printers, it became possible to design custom twisty puzzles enabling the development of much more complex and diverse designs. Many of these, such as the elite Skewb (5) and Skewby Copter plus (9) have subsequently moved into mainstream mass-produced items. The master Skewb, for example, was invented by Katsuhiko Okamoto in 2003, remaining a single copy until mass produced in 2011. The Elite Skewb was designed by Andrew Cormier in 2009 with a 3D printed version by Mohammed Badir and mass produced by MF8 in 2018 and the Skewby Copter plus by Diogo Sousa and mass produced by MF8 in 2016.
Videos
and articles exploring 3D printed design can be found here, here and here. The result is an active race,
among puzzle designers to define the cutting edge of the art.
Fig 3: Computer design tutorial (Grégoire Pfennig), with composite images of his
33x33 design (see 1, 2) pre-production
composite image of the MF8 Twins cube Mar 2019 (now mass-produced fig 1(7))).
Complementing
the mass-produced items available, from US puzzle shops to Aliexpress, is a diverse community of
puzzle building enthusiasts who frequently market their creations in boutique
outlets, as illustrated below. These give expression to the potentially
unbounded limits of human creative ingenuity.
Fig 4: Custom designed cubes: (a)
David Pitcher’s Andromeda plus jumbling cube based on the
geometry of the pentagonal icositetrahedron sharing
properties with 3 and 8 in fig 1. (b) Greg’s Daffodil cube. (c) Diogo Sousa’s Bubblarian massively corner-turning
dodecahedron (d) The Gigshexaminx ingeniously made by cutting down
a Masterkilominx (4x4 corners-only megaminx) into cubic symmetry. (e) Grégoire’s
world record holding 33x33 cube
available for 3D printing pre-order for Ř15,200. You can see Greg assembling it by hand here. (f) David Pitcher’s Star of the Seven, RCP’s Duelling tetrahedra and David Pitcher’s Crazy Daisy. (g) Eitan
Cher's Radio Cube 3, a cubic cut-down of Jason
Smith’s face-turning icosahedron Radiolarian 3 (h), $1100 US at Shapeways.
Groups, Commutators, Orbits and Algorithms
Twisty puzzles are structures composed of geometrical corners, edges and faces which remain intact under a system of rotations in three dimensional space. The overall geometry of the structure is often a regular 3D solid such as a cube, or polyhedron, but the operations may not conform to the geometry of the whole structure. For example, the three cubes in fig 2 have three different sets of rotational operators the first 6 on cubic faces, the second and third 4 tetrahedral axes and the fourth having 8 oblique axes of edge rotation.
Twisty puzzles are determined by four key factors: (1) The axes of rotation. (2) The slice planes perpendicular to these. (3) The overall geometry defining the boundary of the puzzle. (4) The colours or patterns on the surface. The first three together determine the shapes of each of the puzzle pieces. The same axes of rotation can have a varying number of slice planes and varying positions, generating both the NxN series of puzzles and variants with additional centre pieces. The overall geometry and its inclination to the rotational axes also define a diverse series of shape mods for every axis type, in which dualites e.g. between face, edge and corner rotations correspond to geometrical dualities e.g. cube <-> octahedron, cube <-> tetrahedron and dodecahedron <-> icosahedron.
It is thus possible for a given puzzle's rotational core to morph into several structural geometries (fig 18) and even for a puzzle to be able to be interpreted in terms of two inconsistent geometries. For example, the Mastermorphix, fig 1 (14), is both an edge-turning tetrahedral version of the copter cubes fig 32 and is a rotational morph of the standard 3x3 face-turning Rubik cube.
The
rotations form a group under composition (performing one after the other). A
group is a set with an associative binary operator, where every pair of elements c can be multiplied to form p*q, there is an identity (staying still – nil rotation) and every
element p has an inverse p’ = p-1 (the reverse rotation). However, in
contrast with multiplication of numbers, where 3*2 = 2*3 = 6, groups don’t have
to be commutative, so in many groups p*q
≠ q*p.
Fig 5: A match box ends up with
different orientations if the order of rotations is reversed.
Rotation
matrices do not compose commutatively if their axes or or orientations are
different. This is a basic property of matrix multiplication since:
![]() .
.
In the
case of the 3x3 cube, we can describe the group G in terms of six 90o
rotations of the six faces
G = {L, R, U, D, F, B). We don’t
need to include the centre slice rotations because we can keep the centres
fixed. The identity I represents standing still and each rotation R has an
inverse R’ going in the opposite direction. G also contains a subgroup G2
consisting of each of the 180 o double rotations G2 = {L2, R2, U2,
D2, F2, B2), where R2=R*R.
Fig 6: (1) Orbit set of the 3x3
Rubik under the 180
o rotation sub-group G2 contains 2
complementary braided tetrahedral corner orbit sets (cyan and blue) and 3
braided edge orbit sets (red, yellow and green). By contrast, the full 3x3 90 o rotation group G. (2) has fully entangled edge and corner
orbit sets. The central slice moves in (1) & (2) can be factored out
because the centres can be assumed fixed because they are equivalent to a pair
of face moves and a reorientation of the whole cube. (3) The full group for the
4x4 cube is fundamentally more complex in its entanglements, because all edge
pairs can be mixed and the inner slice moves cannot be factored out because the
four centres in each face can also be arbitrarily mixed.
The
orbit of a puzzle centre, edge, or corner is the set of other locations it can
be carried to by the composed rotations. In some puzzle groups the orbits are
braided into discrete interlacing subsets, rather than one tangled whole, so
that several pieces are confined to distinct braids and remain relatively
ordered, while in other groups the orbits are chaotically entangled in the
sense that any type of piece can end up in any of the possible positions for
that type – a state of maximal entropy or disorder. For example, the 3x3 Rubik
has both its edge and corner orbit sets fully entangled in G but has three
braided edge orbit sets and two braided corner orbit sets in G2.
All
twisty puzzles are an exercise in unravelling disorder, so braided orbits are
more amenable to intuitive solutions that exploit their symmetries, while
entangled orbits require stringent algorithms to avoid re-mixing the orbits.
Consequently, it only takes a few moves to get a puzzle scrambled in a way
which takes a much larger number of moves to solve.
Key to
finding moves which avoid re-scrambling solved parts of the puzzle are the
commutators. Since the group is non-commutative, the closest elements to the
identity are those that correspond to the discrepancy between p*q and q*p, for example pqp’q’ = pqp-1q-1 = (pq)(qp)-1.
These often move only a few pieces because, for the rest, the rotations cancel
out. In all twisty puzzles the commutators are the key to solving the endgame.
In the case of the 3x3 Rubik, FRF’R’ cycles 3 edges and flips and rotates two
pairs of corners. More generally a derived commutator is any expression where
the net power of each rotation is zero modulo 4, since 4 90o rotations
are a complete revolution and thus the same as standing still, for example the
derived commutator RUR’URU2R’ of fig 7 permutes edges and corners only on the
top face. One can also combine a sequence of rotations r, which move pieces into the domain of a commutator c to form a compound commutator rcr-1.
Fig 7: (1) The elementary commutator F R F’ R’ swaps two
pairs of corners also rotating them and cycles thee edges. (2) The derived
commutator R U R’ U R U2 R’ swaps and rotates diagonal corners and cycles three edges
on the top face. Differing powers of 2 or 3 of these combined with additional
moves can be used to cycle edges only, corners only or rotate corners, enabling
the fin al layer to be solved without scrambling the reminder. (3) The
elementary G2 groups braided orbits make it much easier to solve, even using
only G2 moves, although the elementary commutator cycles two sets of 3 corners
plus 3 edges, so is not amenable to separate edge and corner moves on powers,
but the compound move U2 R2 F2 U2 F2 R2 U2 F2 can be used
to swap pairs of edges.
For
example, the layer method for solving the 3x3 Rubik is:
(a) To make free rotations to bring
the bottom layer (e.g. white) edges to form a cross.
(b) Pair up the bottom layer corners
with their second layer edges, making suitable rotations of the corners, and/or
flips of the edges, using the relevant column and top level as workspace. Move
the pair into position.
(c) Apply the basic commutator
combined with additional moves to position and rotate the corners and edges e.g.
using the basic commutator powers of 2 on edges and powers of 3 on corners.
Fig 8: Example algorithms for
solving the 3x3 cube.
For
solving the last layer, there are a number of additional algorithms, for
example
1. U R U' L' U R' U' L cycles LUB,
RUB and LUF corners anticlockwise with the inverse
L' U R U' L U R' U' cycling clockwise
2. B2 D' (F R F' R')3 D
B2 swaps corners BUL <-> BUR & FUL <-> FUR
3. The pair of algorithms rotate
corners, as long as one of each is applied, as each scrambles inversely
L D2 L' F' D2 F clockwise on UFL, e.g. followed by U F' D2 F L D2 L' U' anticlockwise on UFR
4. F2 U L R' F2 L' R U F2 cycles edges
UF, UL and UR clockwise, with the inverse cycling anticlockwise.
5. F R' F' R' F2 L D R D' L' R' F2
R2 flips two edges FU & RU.
6. F2 D' F' D F' R2 B U' B' R2 swaps
the ULF-URF corners, and the LU-FU edges.
 Notably:
1, 2, 3, 5, have net power zero and so 1, 3, 5 are derived and 2 is a compound
commutator.
Notably:
1, 2, 3, 5, have net power zero and so 1, 3, 5 are derived and 2 is a compound
commutator.
In
addition, for 3x3 supercubes
such as the "Rangitoto" cube right, where the centres have orientation, example
additional algorithms are:
1. (R U
R' U)5 rotates the U centre 180o.
2. F B' L
R' U D' F' U' D L' R F' B U rotates the U centre 90o clockwise and the
F centre 90o anticlockwise.
As the 2x2 cube has moves identical to the 3x3 with edges omitted, corner
algorithms 1, 2, 3 and 6 provide a basis for solving the 2x2 cube. Note that 6
provides for an odd-permutation corner swap.
The
total possible number of configurations is 8! x 37 x 12!/2 x 211
~ 4.32 x 10^19, since there are 8! ways to arrange the 8 corners, 3 ways to arrange 7 of the 8
corners (the last is locked to the 7), 12!/2 ways to arrange the 12 edges (half
of 12! because edges must be in an even permutation when the corners are) and 11
of the 12 edges can be flipped independently. If centre orientation is also counted,
as in the picture cube (21), there are 46/2 ways to orient the
centres since an even permutation of the corners implies an even number of
quarter turns of centres as well. Since we have factored out 3 rotations of the
last corner, 2 or the even edge permutations and 2 for the last edge flip there
are actually 3.2.2=12 times as many possible arrangements of the disassembled
pieces than the rotations provide. There are thus 11 additional sets of
‘shadow’ configurations forming unsolvable positions in the orbit sets.
God’s
algorithm is the procedure to bring back Rubik’s Cube from any random position
to its solved state in the minimum number of steps. Complementing this is the
notion of the diameter, the minimum number of moves that can get any position
to the solution. If one counts the number of distinct positions achievable from
the solved state using at most 17 moves, it turns out that this number is
smaller than 4.3_1019, giving 18 as a lower bound.
In 1992
Dik Winter established a 20 face turn (either 90 or
180 turn) solution for the 'superflip' (fig 16) where
all edges are correctly positioned but flipped. The most scrambled state is
thus far from random! In 1995 Michael Reid proved that this solution was
minimal. A slightly different position was found with a minimum number of 26
quarter turns or 20 face turns. The following superflip
sequence has the minimal 20 moves in the face turn metric, though it requires
28 quarter turns: U R2 F B R B2 R U2 L B2 R U' D' R2 F R' L B2 U2 F2. This one
has 24 quarter turns (but 22 face turns): R' U2 B L' F U' B D F U D' L D2 F' R
B' D F' U' B' U D'. When the
superflip is composed with the "four-dot"
or "four-spot" position, in which four faces have their centers exchanged with the centers
on the opposite face, the resulting position may be unique in requiring 26
moves under the quarter turn metric.
Finding
an upper bound requires a different kind of reasoning. The usual solution
algorithms can take between 50 and 100 moves.. A breakthrough, using descent
through nested sub-groups was found by Morwen Thistlethwaite. Details were published in Scientific
American in 1981 by Douglas Hofstadter. Thistlethwaite's
method differs from layer algorithms and corners first algorithms in that it
does not place pieces in their correct positions one by one. Instead it works
on all the pieces at the same time, restricting them to fewer and fewer
possibilities until there is only one possible position left for each piece and
the cube is solved by working successively down through subgroups of G:
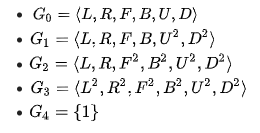
By 1980
Thistlethwaite had established that his algorithm
could solve any position in 52 moves (Kaur 2015). You can access a Matlab version of Thistlethwaite’s
algorithm
extended by the reduction method (see below) to the 4x4 case.
In 1992 Herbert Kociemba
improved Thistlethwaite’s algorithm by reducing it to
a two-phase algorithm requiring only the subgroups G0, G2,
and G4. A freeware version is available from Kociemba’s
home page. Using Kociemba’s ideas,
Michael Reid announced in 1995 that he had improved the upper bound to 29 face
turns. There is an open source GCC version downloadable here.
At
about this time, Richard Korf (1997) introduced a new
approach. A GCC open source version of this algorithm can be found here. Instead of using a fixed
algorithm, his strategy simultaneously searched for a solution along three
different lines of attack. IDA* is
a depth-first search that looks for increasingly longer solutions in a series
of iterations, using a lower-bound heuristic to prune branches once a lower
bound on their length exceeds the current iterations bound. It works roughly as
follows. First he identified a number of sub-problems that are small enough to
be solved optimally:
1. The cube restricted to only
the corners, not looking at the edges
2.
The cube restricted to only 6 edges, not looking at the corners nor at the
other edges.
3.
The cube restricted to the other 6 edges.
The
number of moves required to solve any of these sub-problems is a lower bound
for the number of moves you will need to solve the entire cube.
Given a
random cube C, it is solved as iterative deepening. First all cubes are
generated that are the result of applying 1 move to them. That is C * F, C * U,
… Next, from this list, all cubes are generated that are the result of applying
two moves. Then three moves and so on. If at any point a cube is found that
needs too many moves based on the upper bounds to still be optimal it can be eliminated
from the list.
Although
this algorithm will always find optimal solutions, it is not known how many
moves this algorithm might need. On average, his algorithm appeared to solve
the cube in 18 moves. There was, however, no worst-case analysis, and so the
upper bound held still at 29. Note also that this method uses methods requiring
complex tables that would remain opaque to a
human solver.
In
2006, Silviu Radu reduced
the upper bound to 27. The next year, Gene Cooperman brought it down to 26 (Kunkle, & Cooperman 2007). Tomas Rokicki
(2007, 2008, Rokicki et al. 2014) then entered the
picture, reducing the upper bound to 25 in March 2008. Working with John Welborn, he had it down to 22 by August 2009. Finally, in July
2010, Rokicki announced an upper bound of 20, the
established value of the lower bound and therefore the long-sought-after value
of God’s number (van Grol 2010). Evolutionary methods
have also been applied
(El-Sourani, Hauke,
& Borschbach 2010).
Other
advanced methods for rapid speed-solving of the 3x3 such as CFOP, Petrus, ZZ and Roux abound among speed cubing
communities. Often after solving the first 2 layers F2L, these separate the final layer
into orienting the last layer OLL and then permuting git PLL. Another major question has been to find out whether
God’s algorithm is an elegant sequence of moves that can be easily performed by
humans or an arcane program requiring brute force computation.
Runs of
Thistlethwaite's algorithm quickly display the
relationship of the number of moves required to scramble compared with the
larger number of those needed to solve. The ‘T Solution’ is Thistlewhaite,
the ‘O Solution’ is an optimal in terms of God’s algorithm one at: https://rubiks-cu.be/. For the T Solution 7 moves is a scramble,
but the O Solution appears to mount a search for scrambles of less than 10
moves to find a precise inverse:
Scramble (7 moves): L2,U,L2,U',F2,L2,R
T Solution (31
moves):
U',F2,U,L,U2,F,U2,L2,U2,L2,F,L',F2,U2,L,B2,L',F2,L2,R',U2,L2,F2,R2,B2,L2,B2,U2,B2,R2,D2
O Solution (7 moves): R',L2,F2,U,L2,U',L2
Scramble (10 moves): B,F2,R',B2,U',D',L',R',D,L2
T
Solution (25 moves):
L,R,U,D,L',D2,B2,D2,R,B,U2,L2,B2,L,U2,D2,R,U2,B2,U2,F2,R2,B2,L2,F2
O Solution (19 moves):
R,B',R',D',L2,B,D2,B2,R,B2,L,B,U,D',F2,U,B2,D,F2.
Scramble (12 moves):
U2,D2,L,F',B2,R,U,R',D2,F2,U',L2
T
Solution (28 moves):
L,F2,U,L,F,U2,D2,F,D2,L',F,L',U2,F2,L,F2,L2,F2,U2,R',F2,L2,D2,R2,U2,L2,B2,F2
O Solution (20 moves):
L,D',L2,F2,D2,L2,B',U,L,B',D2,L2,D',L2,D',R2,F2,R2,B2,U'
Scramble (15 moves):
B2,R2,F2,R2,B,L2,R',U',L2,D2,B2,R,U2,L2,D
T
Solution (30 moves): R,D,F2,L',U',F',R',B2,D2,L',F,L,F2,L',D2,L,D2,L,D2,L',F2,U2,F2,D2,R2,F2,U2,F2,U2,D2
O
Solution (20 moves):
D,B',L,U,D2,F2,R,L,F,R,L',F,D',B2,D,R2,U',D2,F2,R2
If we restrict to scrambling and solving using
only 180o turns (our group G2
in figs 6, 7 and Thistlethwaite’s G3), we find that the Thistlethwaite algorithm can solve in many fewer moves than
the scramble, indicating intrinsic ordered simplicity of the solution which
needs only the G3 component, but the optimal solution can’t
recognise this route:
Scramble (15 moves):
B2,U2,B2,D2,L2,B2,R2,L2,U2,R2,D2,B2,U2,L2,R2
T Solution (11
moves): L2,B2,L2,U2,F2,U2,L2,D2,F2,R2,F2
O Solution (20 moves):
D,R',B,U2,F,U,D',B2,U2,F,D,B2,U,L2,U2,R2,B2,D,B2,U'
Scramble (15 moves):
F2,R2,U2,D2,F2,R2,L2,F2,L2,F2,U2,B2,R2,F2,R2
T Solution (7
moves): L2,B2,R2,U2,D2,F2,D2
O Solution (20 moves):
F2,U,L,B,R2,F',U,D',B2,U,B,L2,U,R2,F2,B2,D',R2,U',L2
Scramble (30 moves):
U2,D2,F2,D2,R2,F2,B2,R2,D2,F2,D2,L2,U2,F2,L2,D2,U2,D2,R2,F2,D2,U2,L2,R2,B2, U2,F2,B2,F2,U2.
T Solution (8
moves): L2,D2,B2,L2,D2,L2,U2,F2
O Solution scramble too long for the GUI
One can contrast this with the much longer, manual
solution by Antonio
Vivaldi using the algorithm (4) in fig 7. Because of the
braided corner orbit sets, the corners can quickly be placed by basic
rotations, but the edges then need to be positioned by pairs of parity flips
using algorithm (4).
Overview of the Puzzle Set
To
explore the complexity dynamics, let’s first examine the representative puzzles
in fig 1, and provide some pointers to the solutions. This will both serve to
enable anyone to actually solve the puzzles themselves and provide a view on
the varieties of dynamics they induce.
A: The
Rubik N xN xN Series
The straight Rubik face turning cubes fig 2 (1)
and fig 1 (9, 1, 10, 11) show the 2x2, 3x3, 4x4, 5x5 and 9x9, form a series
leading up to the very large 33x33 example fig 4(d). The 2x2 is effectively
identical to the 3x3 with edges and centres removed and uses a reduced set of
the 3x3 algorithms. All the NxN for N even have no fixed centre determining
the relative orientations of the coloured faces, so the correct spatial parity
has to be determined by inspecting the corners before beginning.
 Number
of Configurations
Number
of Configurations
Fig 9: Log10 plot showing diverse geometries
and super-exponential rise of configurations for NxN
cubes (blue) and super-cubes (red).
As a result of their varying parities, the number
of configurations for odd and even NxN
cubes differs. Let n=(N-1)/2
for N odd, n=N/2 for n even:
Odd
N: 12 edges with 2
orientations each (12! * 2^11), 8 corners with 3 orientations each (8!/2 *
3^7), n-1 orbits of 24 edge wings ((24!)^(n-1)), and n^2-n different orbits of
24 centers, all of which are made up of 4 pieces each
of 6 types ((24!/4!^6)^(n^2-n)). Thus
the total number of positions is
12! * 8! * 24!^(n^2-1) * 4!^(-6n^2+6n) * 2^10 * 3^7. For this family the
existing puzzles are n=1 (3x3x3, with 4.325 * 10^19 positions), n=2 (5x5x5,
with 2.829 * 10^74), and n=3 (7x7x7 with 1.950 * 10^160), n=4 (9x9x9 with 1.417 * 10^278), to n=16
(33x33x33 fig 4, with 1.870*10^4100).
Even
N: 7 corners with 3
orientations each (7! * 3^6), n-1 orbits of 24 edge wings ((24!)^(n-1)), and
n^2-2n+1 orbits of 24 centers, each of 4 pieces in 6 colors ((24!/4!^6)^(n^2-2n+1)). The total number of positions here
is 7! * 24!^(n^2-n) * 4!^(-6n^2+12n-6) * 3^6. The puzzles in this family that
have been constructed are n=1 (2x2x2, with 3.674 * 10^6 positions), n=2 (4x4x4,
with 7.401 * 10^45 positions), and n=3 (6x6x6, with 1.572 * 10^116 positions).
For the supercube cases,
where all pieces are distinct and orientable, we have 12! * 8! * 2^(-n^2+n+21)
* 3^7 * 24!^(n^2-1) for N odd and 7!
* 24!^(n^2-n) * 3^6 * 2^(-n^2+2n-1) for N
even.
Solving
the NxN Series
There are two approaches to solving the NxN series. The first is a layer by layer approach as for N = 2, 3, which becomes increasingly
more tedious for increasing N. The
4x4 introduces parity issues both due to 3D spatial parity inversion of the
face colours since there are no fixed centres and due to odd permutations
generated by the slice moves so that a single pair of edges can become flipped
or two edges become swapped. The second type of parity issue also occurs in the
5x5 in which just one edge can be flipped.
Fig 10: The 4x4 cube has
three types of elementary commutator involving both slice and face moves, each
of which has a pair of cycles. (1) F R F’ R’ swaps two pairs of corners and
cycles three edge pairs, as with the 3x3. (2) F r F’ r’ has a 5-cycle each of
edges and faces. (3) f r f’ r’ has two 3-cycles of faces. Derived commutators
can simplify these to single cycles. (4) F R F' L' F R' F' L cycles 3-edges,
(5) F r F' l' F r' F' l cycles 3 faces. (6) F r F' L' F r' F' L cycles 3 edges.
The second approach, which becomes ever more
essential as N increases, is
reduction of the larger cube to a 3x3 by: (1) Positioning the centres, (2)
pairing up the edges and then (3) solving the resulting layout as a 3x3. This requires
only learning a few simple positioning algorithms. Since the centres of a given
face are identically labelled the solution needs only to position each type of
centre into any of its positions, so for very large n cubes, the centres can be placed in sets of convenient patterns.
Pairing the edges into a solution set is more demanding although there are
fewer of these as they are distinguishable.
4x4
Reduction: For the 4x4 reduction we
have the following sequence of algorithms. Here small letters are the slice
moves and capitals the face moves.
Fig 11: (1-5) Stages in
reducing a 4x4 to 3x3 illustrated from the solved cube. (6) Reduced cube.
The reduction begins with moves which position
centres in the correct face, allowing the other pieces to remain scrambled and
then pair the adjacent edges together without positioning them on the cube,
leaving a 3x3 solution to complete, shown in the stages in fig 11:
1. To
fix centres on the U face, apply U to put an incorrect piece in Ulb from one of the side faces,
r U r' moves Frd -> Ufl also placing the incorrect Ulb
in Fru. Note this is actually a 4-cycle. Non-centre
pieces are freely scrambled.
Alternatively, r2 U r2 moves Drb -> Ufl also placing the incorrect Ulb
in Drf.
2. If
you find your parity is wrong at this point, u2 R2 L2 u2 will swap the L and R
centre sets keeping other centres fixed.
3. To pair edges, find any pair of edge pieces that have the same
colours, but are not yet adjacent. Use face moves only to place one at FDr and the other at FUl so that a
single r will match them correctly (i.e. not relatively flipped). Find
the piece with colours matching FUr,
and place it at FRd using
only face moves. If this is not possible, then put any unmatched piece there. Then
r U' R U r' U' R' U will
pair UFl and DFr to UFl and UFr. Notice this disturbs a third
edge set, forming a three cycle. You should
eventually arrive at 3 unmatched edges which can be placed in the three cycle
positions and simultaneously matched together. If needed, U2 r' U2 r' U2 r' U2 r' U2 r' U2 will cycle DFr > UFr > UBr > DBr > DFr to free 3 edge pairs, while pairing UFl
and DFr. All these moves cancel out all slice moves,
so the centres remain in position.
4. To
resolve edge parity issues: r' U2 l F2 l' F2 r2 U2 r U2 r' U2 F2 r2 F2 double
flips UFl & UFr edges
5. F l
B L2 B' l' B L2 B' F' l' D2 U2 r' D2 U2 l' d2 l2 d2 also swaps edges UFl and UBl.
6. Complete
using a 3x3 solution.
The
extension of the Thistlethwaite algorithm to reducing
the 4x4 results in much longer sequences of moves to find the solution:
Cube Dimension:
4 Solving Method: 423T45
Scramble (7 moves): l2,U,l2,L',b2,l',d
Solution (160 moves): U2,B,l,U,l',U2,r2,U,r2,d,R,d',R,B,u,R,u',L',R,d2,R,d2,D,l,D,l',D',L2,b,D,b',D2,b,D,b',D,F,u,L,u',L',F2,u,L,u',L,
B2,d,L,d',L2,F,u2,B,u2,B',F2,u2,B,u2,D2,L,B2,U2,u,F',U,F,u',F',U',D,L',R2,D',L,B2,b,L',B,L,b',L',B',L,R,F',U2,L,F2,r,R2,D',R,D,r',D',R',
U',D,L',B2,U,F',L',F,U2,u,F',U,F,u',F',U',F,R2,F,D,L,D,l,U',L,U,l',U',L',U,L2,R',U,L2,U2,L,D2,F,L2,R,F',R',B2,R,D2,R',B2,R,U2,L,R2,U2,
B2,U2,B2,L2,U2,R2,B2,R2,U2,B2.
Fig 12: Stages
in reduction of the 5x5 cube with additional p[arity moves.
 5x5 Reduction: The situation for the 5x5 reduction is similar to the 4x4 but more complex to complete. An estimate
of the number of moves involved derived from the world record solve by Feliks
Zemdegs in 2018 of 37.93 secs is 228 moves not counting whole cube rotations,
as shown in fig 13.
5x5 Reduction: The situation for the 5x5 reduction is similar to the 4x4 but more complex to complete. An estimate
of the number of moves involved derived from the world record solve by Feliks
Zemdegs in 2018 of 37.93 secs is 228 moves not counting whole cube rotations,
as shown in fig 13.
Fig 13: Felix Zemdeg’s
world record 5x5
solve.
The algorithms follow closely the 4x4
reduction and need to be followed in sequence to move affected pieces clear of rescrambling. The centres are now of two
types: edge and corner:
1. To fix the centre edges use r U r' to
send Fr -> Uf
and r2 U r2 to send Dr -> Uf. This is
another 4-cycle but different from the 4x4 example and will scramble edge
corners.
2. To fix the corner edges, use r' F' r F'
r' F2 r to send Fur -> Ufr and r2 D' r2 D' r2 D2 r2
to send Drf -> Fur.
3. To pair edges (1), find any central edge piece and any lateral
edge piece that has the same colours, but which are not yet adjacent. Use face
moves only to place them so that the centre edge is at UF and the right or left
side edge is at DFr or DFl.
Make sure that the pieces are is oriented so that that a move of the r or l
layer will line the two pieces up correctly. Place an unmatched piece at FRu or Flu. Use r U' R U r' U'
R' U to pair UF and DFr to UF and UFr.
Notice this disturbs a third edge set, forming a three cycle. For the left edge piece apply the mirror
image move l’ U L’ U’ l U L U’. You should
eventually arrive at 3 unmatched edges which can be placed in the last three
cycle positions and simultaneously matched together. If needed, U2 r' U2 r' U2 r' U2 r' U2 r' U2 will cycle DFr > UFr > UBr > DBr > DFr to free 3 edge pairs, while pairing UFl
and DFr. All these moves cancel out all slice moves,
so the centres remain in position.
4. To swap opposing (unpaired) edges UFr
& DFr use l' F2 l' F2 D2 l' D2 r F2 r' F2 l2.
5. To flip two edges use r' U2 l F2 l' F2 r2 U2 r U2 r' U2
F2 r2 F2.
6. To swap FUl & BUr
as well as FUL & BUR use F2 R r U2 R r U2 R' r' F2 R' r' U2 R' r' U2 R r U2
R' r' U2 R2 r2.
7,8. Additional moves to correct edge
parity are R2 r2 B2 U2 L l U2 R' r' U2 R r U2 F2 R r F2 L' l' B2 R2 r2 and/or
L' l' U2 L' l'U2 F2 L' l' F2 R r U2 R' r' U2 L2 l2.
A solution video can be found here. You can see a variety of pattern algorithms here.
N xN Reduction
Generalizing to larger Rubik cubes
involves using the principles of the above reduction methods, as adapted below.
The algorithms below are precise and non-scrambling but take a very large
number of moves ~N3, so there are intuitive ways of speeding up the
placement of the centers in patterns. A
good way of exploring this process in detail is by watching tutorial videos of
the 5x5x5 and
9x9x9 solutions, to show how the 5x5 solution extends to the
9x9. There is even a lego robotic demonstration of solving the 9x9, with a review and lego mindcuber kitsets.

Fig 14: Left: 9x9 face moves placing UmRn m,n = 3,5 (above) and 2,4 (below) in a 3-cycle, 9x9 Rm edge pairings m = 4,3 again forming a 3-cycle. Above centre: 9x9 solution intuitive stages (Left) U (top) is
being used to fill F (bottom) with centre pieces in vertical strips, and
contiguous patterns. Edge pairing (top right) involves temporary displacements
of the centres and algorithms (bottom right) to complete the last stages. Below:
Lego robotic 9x9 solver. Right: Decomposition of the MoYu 9x9. You can also see a full 13x13 solution and another. A time-lapse 17x17 solution. 17x17 patterns.
Here follows a specific algorithmic
method for N xN cubes of arbitrary size. It uses
refined improvements of the centre moves which can position all the centre
pieces without scrambling. The edge pairing are essentially the same as 4x4 and
5x5. Additional parity fixes may be required, as illustrated above for 4x4 (even
case) and 5x5 (odd case). We denote L and R slices by L,L2, … , Ln-1,
Rn, Rn-1, … , R2, R and DU in the same
way.
(a) Centres: For very large cubes, one
can use two adjacent faces, say U and F building horizontal rows of a given
colour in U and then rotating them and slotting rows vertically into the F face,
also rotating and moving patterns that will add centre pieces without
disruption.
1. Solve the centres of two opposite faces say F and then D, using U
as a workspace, by matching up all of the centre pieces of that colour.
2. Solve another two adjacent centres on the puzzle using the freedom
of the 4 unsolved centres on the puzzle.
3. Use commutators and puzzle knowledge to solve one of the last two
centres, leaving the last centre solved.
4. Alternatively use the commutators below throughout.
a. Find any centre piece edge that belongs on the U face at UBmRn. Hold the cube so that it lies
on the D face.
b. If the piece is in the front face, turn F to put the piece at the
top right.
If it is in the bottom face, turn D to
put the piece at the front right.
c. Turn the U face so that there is an incorrect piece at the back
right location where the piece belongs.
d. From FUmRn to
UBmRn: Do Rn U' Lm' U Rn'
U' Lm U
From DUmRn to
UBmRn: Do Rn2 U' Lm2
U Rn2 U' Lm2 U
e.
Repeat a-d until all centre pieces in
the U face are correct.
f.
Repeat for each of the faces.
(b) Edge sets The edge sets although
fewer are all distinguishable and their rearrangements have to preserve the
centres over the process, so their matching up is more demanding:
1. First 8 sets: Temporarily disturb the solved centres to match edge
pieces and complete 8 edges, placing each solved edge on to the top and bottom
layers of the cube.
2. Last 4 edge sets: After realigning the centres, use algorithmic
combinations to complete the final 4 edges
3. Alternatively use the algorithm below throughout to match up the
edges sequentially from the centre to form matching pairs.
a. Find any edge piece that is not yet matched up with its UF middle
edge set, completed up to but not including UFRm,
starting from the middle edge.
b. Find the matching middle edge piece. Use any face moves to bring
it to the DFRm location, correctly flipped
so that a single Rm slice will match it.
c. Do Rm U' R U Rm U'
R' U.
d. If there is no other unmatched inner edge, then do U2 Rm U2
Rm U2 Rm U2 Rm U2 Rm to
make some new unmatched inner edge pairs and try again.
e. Repeat until all edges are matched up with the middle edge sets.
(c) 3x3 Solution as above.
Since corresponding centres can be
exchanged by a face rotation, the centre solutions would also solve the
distinguishable centres of the supercube, and since
the edges and corners are always distinguishable these algorithms combined with
the 3x3 supercube solution above are a complete
solution to the NxN supercube
as well. We thus have a quadratic order NxN solution proportional to (N-2)^2+12(N-2)+20 i.e. O(N^2).
While the number of conformations fig
10, grows super-exponentially roughly with O(24!^(2n^2)), the time taken to solve increasingly large NxN cubes grows much more slowly. Record times for N = 3, 3.7 secs; N = 4, 21.42 sec; N = 5, 37.93 sec; N = 7, 107 sec; N = 9, 13 mins 37 sec and N = 13, 86 mins 41 secs, giving a power law of t
~ N^1.98. The times for Yusheng Du’s N = 2-7 average solutions gives a similar figure of t
~ N^2.42, both roughly quadratic O(N^2).
Fig 15: Left: Solution times Yusheng Du current world 3x3 record
holder. Right: Power law curves for (a) record times, (b) Yusheng Du’s average
times and (c) the number of moves to achieve record solves.
The number of moves required likewise
grows even more slowly. A reconstruction of Yusheng Du’s world record 3.7 sec 3x3 solve shows it
taking 28 moves, Felix Zemdeg’s 4.22 sec 3x3 solve took 38 moves, the Thistlethwaite
4x4 solve above took 168 moves, Felix Zemdeg’s record
solve for the 5x5 taking 37.93 secs involves 228 moves, not counting whole cube rotations. An
estimate of the 13x13 from the video above is around 781 moves, giving a power
law of m ~ N^1.26.
In 2011 Erik Demaine
and co-researchers (Demaine et al. 2011), discovered
a general algorithm for solving the NxN cube of any
size. Demaine’s team started by looking at a method
that humans commonly use to solve the puzzle, by trying to move a single piece,
or "cubie", into the desired position while leaving the rest of the
cube as unchanged as possible. This method is time-consuming, requiring a
number of moves that is proportional to N^2, as noted above. Demaine and his
colleagues found a short-cut. Each cubie has a particular path that will place
it in the correct position. His algorithm looks for cubies that all need to go
in the same direction, then moves them at the same time. Grouping cubies with
similar paths reduces the number of moves required by a factor of around
log N. This means that the
maximum number of moves that will ever be required for a cube of side N is proportional to n^2/log n i.e. O(N^2/log N).
Fig 16: Stages
in the development of the O(N^2/log N) NxN algorithm (Demaine et al. 2011).
Higher-dimensional
Apps: One can also explore a simulation of the four dimensional 3x3x3x3
cube using the downloadable java jar applet available from superluminal software,
using Java
runtime. Two
explanatory videos v1, v2
also overview its properties. There is also a general nD
2x2 and 3x3 java-based
solution program, with a 5D msi
simulator and 5D permutation
counts and a 120-cell
simulator, providing a 4D megaminx
analogue.

Fig 17: Left: The 4D 3x3x3x3 simulator. Centre:
The 5D simulator. Right: The 120-cell simulator.
The number of configurations grows rapidly with
dimension. The 4D 3^4 cube has (24!x32!)/2 x 16!/2 x 2^23 x (3!)^31 x 3
x(4!/2)^15 x 4 = 1.756*10^121 and the 5D 3^5 cube
(32!/2)(60^32)(80!/2)(24^80/2)(40!*80!/2)(6^80/2)(2^40/2) = 7.016 x 10^560. The
5D 7^5 cube has 2.287 x 10^21503 configurations!
B Rubik Shape Mods
Puzzles 2, 18, 19 and 20 in figs 1 and 8
illustrate a variety of so-called ‘shape mods’ of the face-turning 3x3 and 4x4
cubes using the same internal mechanisms and having essentially the same
solutions, with the exception that the centre pieces are generally
distinguishable and have defined orientations, so additional algorithms are
required to place these pieces correctly. Some other pieces may lose their
orientations reducing the total number of conformations.
These puzzles can present a major pattern
recognition task for the solver because the pieces can only be identified by
their shape. The image of (2) above shows that a face turn consists an oblique
corner slice and although the ‘face’ has complete homology with the 4x4 cube in
terms of having four centres, four edge pairs and four corners, many of the boundary
pieces are of only o e colour with no indication of where they match up
colour-wise as is the case with two-coloured edge pieces on the cube. Each
‘face’ actually consists of a triple of colours each of which is shared with
other ‘faces’. The slice moves are also very problematic to keep track of as
there are no obvious landmarks and the shape and colours keep transforming.
Fig 18: (1-3, 5) 'Shape mods of the 3x3 cube. (2) is a 4x4 shape mod. Each are oriented to show their planes of rotation are identical to those of the 3x3 and 4x4 cubes. Their solutions are thus also identical, except that the centre pieces now have an identified orientation, (and position in the 4x4 case) and some other pieces, such as the small corner triangles in (2) lose their orientation. However, when scrambled, these puzzles present a serious pattern recognition problem, as their scrambled shapes (right) are almost unrecognisable. Notice that the 'faces' are now corner sets (2-4), or edge sets (1). (2) and (4) are regular oblique axis morphs, while (3) is irregular and its pieces are entirely asymmetrical. (1) Can be represented either as a face-turning 3x3 cube mod or a tetrahedral edge-turning puzzle. Notice all the rotating sets preserve the arrangement of centres edges and corners on the corresponding 3x3 or 4x4 face. On the Diang Sheng blade rhombohedron (2), the centre is a corner and the actual corners are the large corner piece and 3 small triangles, while the actual edges are the two large faces and the two bi-coloured edges, preserving the 3x3 Rubik face arrangement. 9x9 ghost cube (lower center) and 11x11 bumpsanity mirror cube (far right) illustrate shape mods of arbitrary size, as applies also to the mastermorphix series fig 20. The 4x4 corner-turning octahedron, fig 28 is also a shape mode of the 4x4 cube.
Puzzles (2) and (4) form regular symmetric morphs of the 4x4 and 3x3
cubes with (2) stretched into a prismatic rhombohedron form. These referred to generally as ‘axis’ cubes because the axes of symmetry
of the cube has been reoriented off the axes of the rotation operations. Their
‘faces’ are thus regular, and the pieces on each of the 6 ‘faces’ are alike. By
contrast, the Ghost cube (3) is asymmetrically reoriented, so that all the
pieces are different, as well as being in only one colour, so recognition
depends entirely on shape. There are a variety of other 3x3 shape mods, including the
Fisher and Mirror cubes and other geometries. The solution methods for the 3x3
cases are the same as the 3x3 supercube above in
terms of the centers. However, because some of the
pieces are indistinguishable or don’t have visible orientations in both (1) and
(2) above, the the total number of combinations is less than that of the 3x3 supercube, as we shall show below for Mastermorphix.
For layer solutions of the 4x4 axis cube see: 1. Antonio Vivaldi’s tutorial Part1, Part2 , 2. L M Cubing’s Tutorial , 3. Seppomania’s Parity fix.
The Mastermorphix (1) is exceptional because
it is both a tetrahedral shape morph of the 3x3 cube and is also a tetradedral realization of the edge-turning ‘copter’ cubes
under 180o rotations, complete with corresponding jumbling moves
arising from the 90o rotations. Notice that all the actual cube edge
pieces are the tetrahedral faces, the ‘edges’ are actually the centres and the
corners of a face actually consist of two corners and two ‘centers’.
Hence the super-fip fig 20 flips all the faces on a
given side to make a ‘flower’.
C: The Diverse Geometries of Face and
Corner-turning Twisty Puzzles
We will consider only the analogues of the 3x3
cube in detail, rather than larger NxN systems, to
elucidate how varying geometries introduce new dynamical systems into the mix.

Fig 19: (1) Pyraminx can be thought of as
either corner-turning or face-turning but only corner turning commutators are
useful for solving the puzzle. (2)
The elementary adjacent corner commutator cycles only 3 edges. The algorithm R U
R' U R U R' U cycles three edges on the same level.
Pyraminx Tetrahedral Series
Pyraminx
can be thought of as either a corner-turning or a face-turning puzzle, or both,
but the face-turning moves involve scrambling a majority of the pieces, so the
only elementary commutators of interest arise from compositions of second-layer
corner moves, the first layer being trivial rotations of a single corner piece.
In addition, the three faces next to the corner are not separated by any moves
so are manufactured as a single block.
All turns create even permutations, so every
orbit has permutation parity. Investigation of the elementary commutator 19 (2)
shows that the only permutations generated are a 3-cycle of the edges, meaning
this is purely an edge-moving puzzle solved by the elementary commutator.
Excluding the 3^4 trivial tip positions, there
are 4 corners each with 3 orientations (1 * 3^4), 6 middle edges with 2
orientations each (6!/2 * 2^5), n-1 orbits of 12 edge wings ((12!/2)^(n-1)), a
total of floor((n-1)^2/3) orbits of 12 centres, in 3 centres for each of 4 colours
((12!/3!^4)^(floor((n-1)^2/3))), and ((n-1)^2 mod 3) orbits of 4 centres
((4!/2)^((n-1)^2 mod 3)).
Thus the number of positions is
6! * 2^(5-n-((n-1)^2 mod 3)) * 3^4 * 12!^(n-1+floor((n-1)^2/3)) *
3!^(-4floor((n-1)^2/3)) * 4!^((n-1)^2 mod 3). For the 3x3 pyraminx
with n = 1, there are 7.558 * 10^7
positions, counting both tips and corners, 933120 if only corners are counted
and 11520 if neither these trivial rotations are counted. With the 4x4 master
version with n = 2, we get 2.681 * 10^15 positions, still not approaching the
complexity of the 3x3 cube.
The solution requires only positioning and
orienting the tips and corners correctly in terms of the corner colours using
elementary rotations and then applying either of the 3 cycle algorithms in fig
19.
Fig
20: (1) The same algorithm L2 R2 F2 B2 U2 D2 results is a dual pair of
symmetries in the Mastermorphix and 3x3 cube. (2) The 3x3 superflip in both a cube simulation using the first superflip
and the Mastermorphix, where, despite there being three ‘face pieces’ to a
tetrahedral face, the actual cubic face fig 18(18) has 4 ‘faces’ as actual edge
pieces. Because these pieces have only one colour, but a different shape when
flipped, we get a single coloured ‘flower’. You can apply the first of the
above superflips, which gives the 'flower' with 2
'edge' centres correctly oriented for the single colour, 2 out by 180o and 2 by 90o, followed by the supercube
centre rotations above to orient these correctly. (3) The morphix
series from the pyramorphix n =2 to the n =6 version.
(4) Scrambled mastermorphix. (5) 6x6 reduction solution: (a) The braided version as in 1. (b) Fully scrambled. (c)
All but one centre positioned. (d) Edge pairing. (e) 3x3 solutions. (f) One
corner to be reoriented by a rotation o both this and
an unoriented center (also
a cube corner piece).
Mastermorphix
The edge-turning Mastermorphix
provides an alternative to the corner vs face turns of the pyraminx
which incorporates further interesting properties of the tetrahedral geometry,
which we will investigate in the section on edge turning puzzles, in which the cube’s
90o face rotations become the equivalent of jumbling moves.
The overall polyhedral symmetry is of an
edge-turning tetrahedron, while the underlying rotations are identical to the
face-turning 3x3 cube. This is because the six edge axes of rotation have the
same xyz symmetry of the underlying cube’s face rotations. Thus there is a
complete dual representation in which each tetrahedral edge move is equivalent
to the underlying cubes face moves.
We can thus either solve any morphix
series puzzle as a cube shape mod. However the underlying cube centers corresponding to the six tetrahedral edge pieces
now have distinct rotations while only four of the underlying cube corners
corresponding to the tetrahedral corners have identifiable orientations, while
the other four corresponding to the four tetrahedral centers
do not. The underlying cube edges corresponding to the tetrahedral faces no
longer have two colours but their flipped or unflipped
orientations are identifiable by their reversed states we can see comparing (1)
and (2) in fig 20. The
solution is thus the same as the 3x3 supercube except
the ‘center’ corners have no preferred orientation.
Fig
20 shows these dualities between the tetradedral and
underlying cubic symmetries. In (1) the cross-hatch algorithm for the cube set
up a second kind of colour symmetry in the tetrahedral representation. In (2)
the cube superflip turns all the edges into a ‘rose
flower’ pattern which if the supercube center rotations are applied becomes a single-coloured
flower. There are also NxN versions for N = 2 to 6.
The number of moves is as follows: There are four
corners and four face centers. These may be
interchanged with each other in 8! different ways. Although the puzzle is a 3x3
cube shape mod, there are only 3^4 ways for the corners to be oriented, since
the face centre orientations (which also correspond to the cube corners) are
not visible. There are 12 non-central face pieces. These can be flipped in 2^11
ways and there are 12!/2 ways to arrange them. The three non-central face
pieces of a given colour which correspond to cube edges are indistinguishable.
Since there are 6 ways to arrange the 3 pieces of the same colour and there are
4 colours, there would be 2^11_12!/(3!)^4 possibilities for these pieces. Hence the total is 8! * 3^4 * 12!/2 * 2^11 /( 3!)^4 = 1.236
* 10^15.
Fig 21: (1) The elementary
commutator on adjacent faces swaps 2 pairs of corners and cycles 3 edges. (2)
Swapping an edge pair and a corner pair. (2b) Flipping 2 edges. (3) Cycling three edges (also moving
corners). (4) Cycling 3 corners. (5)
Megaminx Dodecahedral Series
The Megaminx is an
edge-turning puzzle with very similar dynamics to the 3x3 cube. All turns
create even 5-cycles, so every orbit has permutation parity. The elementary commutator on adjacent
faces, like the cube, swaps two pairs of corners and cycles three edges, as
shown in fig 20 (1).
The solution proceeds, as with the 3x3 cube,
first placing the correct edges in the bottom layer, then positioning corner
pieces with their adjacent edge pieces in the five adjacent and then five upper
layers using the same techniques as the cube. See also Jaap’s solution page.
Algorithms as shown in fig 21 can then be used to complete the solution in the top layer. The algorithms are:
 (1) F R F' R', (2) F U R U' R' F' (2b) L U F U' F' L' (flips LU & LF) or L F U F' U' L' (flips LU and RU).
(1) F R F' R', (2) F U R U' R' F' (2b) L U F U' F' L' (flips LU & LF) or L F U F' U' L' (flips LU and RU).
(3) R U R' U R U3 R' U (4) L' U2 R U'2 L U2 R' U'2 and (5) (R' D' R D)2 [ac] U (D' R' D R)2 [c] U' :
The Kilominx (right), which lacks the edges is solved by considering only the corners.
In the general nxn case there are 30 edges with 2 orientations each (30!/2 * 2^29), 20 corners with 3 orientations each (20!/2 * 3^19), n-1 orbits of 60 edge wings ((60!/2)^(n-1)), and n^2-n orbits of 60 centers, in 12 colors of 5 pieces each ((60!/5!^12)^(n^2-n)).
Hence the total number of positions is 30! * 20!
* 60!^(n^2-1) * 5!^(-12n^2+12n) * 2^(28-n) * 3^19. This gives the Megaminx, with n = 1, 1.007 * 10^68 positions and the 4x4 Gigaminx with n =2 having 3.648 * 10^263 positions and the 9x9 Petaminx with n = 4 having 3.165 * 10^997. The Kilominx with corners only can be calculated by
eliminating the edge permutations, and Alexander’s star by eliminating the
corner permutations.
Fig 22: A variety of
polyhedral twisty puzzles including the Great Icosahedron (Right).
The
Alexander Star (top-right fig 22) is equivalent to the Megaminx
without the corner pieces, so is solved the same way considering only the edges
and edge algorithms. Applying the elementary commutator as in fig 23 shows the
puzzle can be solved by elementary edge moves, completed by the commutator
3-cycle.
 Fig 23: The elementary commutator of Alexander’s
Star is sufficient to solve the puzzle.
Fig 23: The elementary commutator of Alexander’s
Star is sufficient to solve the puzzle.
We choose one pair of pieces and fix one. There
are two identical pieces, so we can fix each position exactly two ways, so we
have to divide the result by 2. The number of positions is approximately
(29*(28!/2!^14) * 2^28)/2 or 7.243 * 10^34.
Multidodecahedra
We next look at the solution of the classic Multidodecahedron illustrated in (d) fig 22. This consists of a dodecahedron whose outer pieces are identical to the Master Pentultimate dodecahedron illustrated (a) in fig 22. This evolved into a void face form shown immediately to the right of (a) and then the Multidodecahedron (d), where the void faces reveal a small copy of the set of pieces on one face of a Megaminx in fig 21. The turns induced when a skewb move of the outer pieces is made thus cause a complete internal Megaminx scrambling in simultaneous with the master skewb moves outside.
The Master Pentultimate is a dodecahedral analogue of the master skewb solved in section D, as it divides the dodecahedron into three oblique sections with a single slice move between in a manner which cuts through each outer face obliquely. However, while the skewb cubes have sections rotating on the 8 cube corners, the Master Pentultimate is still making expanded dodecahedral face turns although they cut the faces in a similar oblique manner.
The Multidodecahedron comes in several versions, including the
Bohric adopting a ball form and the MF8 Multiple Ball which omits the corner
pieces.
There is a second type of multiple dodecahedron called the Crystal
Dreidel (c) in fig 22, which in the same way has a Master Pentultimate containing a copy of the Crystal Pyraminx shown in
(b) in figure 22, which is the equivalent of a Megaminx where the face cuts are moved down to the centre and is solved in a similar
manner to the Megaminx. down to the centre. This
puzzle which lacks the skewb edge pieces and is
solved in essentially the same way except the in the Crystal Pyraminx, 5 of the 10 pieces are rotated in each face turn
instead of the 3 in the Megaminx.
Fig
23b: (1) The MF8 version. (2) The Bohric ball version solution naming the 12
faces. First the megaminx is solved as in fig 21. The
ensuing skewb moves leaves the megaminx unchanged in the solved condition. (3) Permuting three edges. (4) Permuting 3
internal floating edge sets, which move together as a unit of a single colour
(this also disturbs other pieces). (5) Permuting three corners. (6) A setup
move is made to swap two pairs of corners followed by the two step move top
causing a corner rotation. The setup is then repeated to undo the swap and the
inverse two step move is made to rotate the second corner in the opposite
direction. (7) Finally sets of 3 faces are permuted. (8-10) Antonio Vivaldi's algorithms work with a slightly different ordering and purpose (11) The puzzle is a Megaminx equivalent encapsulated inside a void Master Pentultimate which rotates on circular rails. In precisely the same way, the Bohric was constructed manually using an MF8 Pentultimate and a Shengshou Kilominx.
The solutions see Marc 1 & Antonio 2 consist of a composite of the Megaminx solution and that of the Master Pentultimate performed in sequence. It might seem counter-intuitive that these two can be solved without scrambling one another, but the skewb moves of the Pentultimate leave the solved Pegaminx intact for two reasons. (a) Key Pentultimate moves involve commutators between non-adjacent faces because the skewb-like arrangement turns half the faces of the dodecahedron up to the middle slice so that the commutators, such as R L' R' L (which equals R up L up R down L down in skewb notation), don’t involve adjacent faces which could scramble the Megaminx. (b) Those that do, undo any Megaminx scrambling, or are matched to moves which do so, by performing their inverse during the process.
The solution thus goes in the following stages, which follow a
sequence so that each stage leaves the pieces that have already been solved
unscrambled, although the earlier moves are not perfect and do scramble other
penultimate pieces:
 (a) Solve the megaminx centres.
(a) Solve the megaminx centres.
(b) Permute the outer edges in 3s as in (3) – R' L R L'.
(c) Permute the floating centre sets in 3s as in (4) – R L' R' BR R L R' BR'.
(d) Permute the corners in 3s as in (5) – R U R' U R U'2 R' U' R U' R' D'.
(e) Orient the corners using the setup move (R'2 L2 R2 L'2)3 to swap 2 pairs of corners to rotate one corner clockwise and
its pair anti-clockwise using U UR as in (6), followed by the setup repeated and UR' U'.
(f) Permute the outer faces in 3s as in (7) – DR'2 L2 DR2 l' DR'2 L'2 DR2 l (where l is the L slice move).
Fig 23c: The puzzle is partly solved . The inner megaminx is solved and the inner faces are matched to it. The outer edges are all solved and the outer faces are part way through. Note the TomZ and mf8 signatures on the correct white face. The rwb corner is accidentally correct.
Antonio's solution uses similar algorithms in a slightly different order for slightly different and clearer more concise purposes.
This is the method I used, with Marc's corner rotations included for completeness.
(b) Swap two pairs of floating centres U <–> F and BR <–> BL, again using commutator R' L R L', combined with
HCH-1moves to bring a pair of faces into position.
(c) Permute edges, U-BL –> U-BR –> BR-B –> U-BL without swapping centres:
–> r' L R' L' r L R L' inverse <– L R' L' r' L R L' r mirror image <– l R' L R l' R' L' R inverse –> R' L R l R' L' R l'.
This move also scrambles outer faces so needs to be done before (d) although it leaves corners unchanged.
(d) Permute faces BL-br-u –> R-u-f –> BR-bl-u –> BL-br-u by
<– l' R'2 L2 R2 l R'2 L'2 R2 inverse –> R'2 L2 R2 l' R'2 L'2 R2 l mirror image –> r L2 R'2 L'2 r' L2 R2 L'2 inverse <– L2 R'2 L'2 r L2 R2 L'2 r'.
This also preserves corners unchanged, so can be done after the corners.
(e) Use the above to swap corner pairs U-BL-BR <–> F-DL-DR and B-DL-UL <–> B-DR-UR – (R'2 L2 R2 L'2)3.
(f) Orient the corners using (R'2 L2 R2 L'2)3 to swap 2 pairs of corners to rotate one corner clockwise and its pair anti-clockwise
using U UR as in fig 23b (6), followed by (R'2 L2 R2 L'2)3 again and UR' U'.

Fig 23d: Far left: A single RU move has both shifted the centre faces from the inner puzzle colours and lightly scrambled the inner megaminx, so that there are pink, blue and red pieces inside the blue pentagon and a red edge and a pink edge and outer face and there are white blue and yellow edges and outer faces on the white pentagon. Centre Left: Edges now in correct position. Towards the end of this process an even number of edges may be in flipped positions. Supposing we want to move a to c but it is flipped. We can instead move it to b and then to c in an HCH-1 move viz bcf –> cfb , ace –> eac , afb –> baf . This will leave e in the a position and c in the e position, obligatory for an even permutation, but b, d and f are back in correct position. We can combine such moves with placing an out of position piece in a cycle to avoid scrambling and undoing this move afterwards. The same thing applies to a flipped move from a to d. Centre: Solving faces. The three outer faces, (a) light green in the cream pentagon, (b) a cream face in the pink and (c) a pink face in the light green. b and c can be directly permuted, but a is in an odd position. However, we can permute as follows ade –> dea, and then fag –> agf. This puts a in cyclic position with b and c where we can do abc –> bca, putting a and c in their correct pentagons. We can then un-permute the first two with c replacing a, viz cgf –> fcg, dec –> cde putting all of a, b and c in their correct positions, leaving all the others unchanged. Centre right: a and g are both in odd positions but we can move a into position g using an HCH-1 move
In both the approaches above, the edge and face permutations can be combined with using the slice moves as a conveyor belt with setup moves that are then inverted after applying the commutator algorithm: M=HCH-1, so that an essentially arbitrary edge or face piece can be placed in position. These can involve a piece we need to place or to put pieces that haven't yet been placed in 3-cycle target positions so good positions don't get scrambled. One can also pre-rotate 3-cycles by an inverse so a new piece, when included leaves all three in the correct position. This means the 3-cycles form an interacting dynamical system which can be used e.g. to flip edges if one or more pairs are inverted or to bring odd parity outer faces into position. Edge pieces will flipped through 180o by being passed using successive cycles round three sides of a triangle, but if you do this, more pieces will get scrambled than the moves in fig 23d. The same reasoning applies for the outer faces, which don't have a flipped condition, but can end up in an odd position, when we can see that a single rotation always moves them in steps of two, thus requiring a compound sequence of three cycles to put them into the correct 'parity'. One can combine chains of 3-cycles linking at a single vertex, in an M=HCH-1 move to swap a flipped or odd parity piece with the one at its destination in a sequence of three 3-cycles that will leave all pieces fixed except for a single odd-permutation swap at [12] in the first 3-cycle, as shown in fig 23d. This converts a flipped or odd parity piece taking another piece just out of position by one move. Ultimately this should end with three pieces in accessible positions which can be cycled as shown. The corners are the only pieces you can pull out, so they can be solved by cheating. The other pieces are all fixed on great arcs like a train of carriages. Beware! The full version puzzle is very sticky to rotate and can derail and split down the middle which is why I have cheated on the corners for now because their moves require the longest algorithms of all.
Number of moves: [ 30! * 20! * 2^(27) * 3^19 ] * [ 12! * 30! * 60! * 2^(27) *3^19 ] = 1.66029e+208.
Polyhedral
Puzzle Simulator
There is a polyhedral puzzle simulator with a
huge number of examples including face, edge and corner turning dodecahedra and
icosahedra, you can download in a Java applet installer here.
Download the current version of Java
runtime if you don’t have it. The puzzle simulator is ideal for
investigating a huge variety of twisty puzzles involving polyhedra such as face-turning icosahedra which are harder to find in physical form.

Fig 24: Above: An MF8 pentagram dodecahedron designed by Eric Virgo
with simulator version. Video solution.
 Face-Turning
Octahedron
Face-Turning
Octahedron
Fig 25: The octagon is a puzzle within a puzzle.
The edges are mounted on a smaller twisty puzzle, sothey can orbit since none
of the pieces in the main puzzle are on the centre of rotation.
The Face-turning octahedron brings with
it some surprising new features and displays features of triangulely
tiled polyhedral like theicosahedral puzzles. The rotational axes are at the
centre of the triangular faces and do not pass through any piece. Consequently,
the puzzle has to be constructed as a puzzle within a puzzle, with an internal
spherical twisty mechanism fig 25 holding the edges in fixed orientation in
relation to the mechanism, with the centres and corners floating latched under
these.
This means (a) that all the pieces are permuted,
but also (b) that an edge’s orientation is determined by its position, as in a
corner-turning Dino cube. You can see this if you try to flip a piece by
consecutive rotations, where successive faces are connected in fours at each
corner, not the threes in the cube and Megaminx, so
an edge can’t be flipped using adjacent faces.
 If we examine the elementary commutator F U F’ U’
as shown in fig 26 (left) you find that, as usual, two pairs of corners are
swapped and three edges cycled, however there are two sets of 5 cycles among
the centres of two colours, in fig 26 red/grey and green/purple. This means
that unlike the cube and megaminx, where comm^6 = I here it takes comm^60 = I, because it takes com^4 to make 2
180o rotations of the corners and 4, 3, and 5 are relatively prime.
If we examine the elementary commutator F U F’ U’
as shown in fig 26 (left) you find that, as usual, two pairs of corners are
swapped and three edges cycled, however there are two sets of 5 cycles among
the centres of two colours, in fig 26 red/grey and green/purple. This means
that unlike the cube and megaminx, where comm^6 = I here it takes comm^60 = I, because it takes com^4 to make 2
180o rotations of the corners and 4, 3, and 5 are relatively prime.
Fig 26: (1) On the
face-turning octahedron, there are cycles of three different lengths in the
elementary commutator F U F’ U’ (U=red, F=green). Two views are shown so all
the permuting pieces can be seen. Two pairs of corners are swapped and rotated
90o (cyan) three edges are cycled (yellow) and two sets of five
faces are cycled. (2) The commutator squared rotates corners by 180o.
(3) The algorithm F U F’ U F U F’ cycles 3 edges on a face (F=green U=red). (4)
The commutator R U R’ U’ (R=white U=red) permutes three corners and two
3-cycles of faces. (5) R' U L' U' L U' R U swaps two corners (U=yellow R=green
L=blue). (6) (r U r' U' r)^5 swaps two centres (R=green U=red).
Unlike the cube rotating faces can interact both
along edges and across corners setting up different kinds of permutations of
the elements.
The most straightforward method of solution is
as follows.
(1) Solve
the edges, keeping the colour scheme consistent with the corners, as the ‘dino’ moves enable one to do this without re-scrambling, as
the final orbits resolve.
(2) Solve
the corners using the commutator as in fig 18.
You can flip a pair of adjacent corners using R' U L' U' L U' R U,
or alternatively do R U' R' U R' L R L' (fig 18).
(3) Position
the centres using a commutator 5-cycle as shown in fig 18. Using (r U r' U' r)^5
(where r means a turn of the middle R layer clockwise, as viewed from the R
face) will move only 2 centre pieces of different colours (fig 26).
Antonio Vivaldi has a tutorial on
the solution. Jaap’s solution
page.
If you tile the faces of the pieces in a
dark-light checkerboard, none of the moves mix the colours. Therefore the
corners have only two orientations, and the edges only one, behaving like a dino cube corner rotation. Furthermore, the centres split
in two sets that don't intermingle. Consequently we have 6 corners with 2
orientations, 12 edge pieces, and two sets of 12 centre pieces. This gives a
combined upper bound of 6!*2^6*12!*12!^2 arrangements. However only an
even number of vertex pieces are flipped (2), the vertex permutation is even
(2), the edge permutation is even (2), the centres come in identical triplets
(3!8) and the orientation of the puzzle does not matter (12 rather than 24
since we fix the orientation of the puzzle by fixing one unique corner or edge,
which has 12 possibilities). The total number of positions is therefore
6!*2^3*11!*12!^2 / 3!^8 = 3.141*10^22.
3x3
Corner-turning Octahedron
Just as the edge-turning mastermorphix is a tetrahedral shape mod of the
face-turning cube and the corner-turning icosahedron is a shape mod of the
face-turning dodecahedral megaminx, the corner
turning octahedra are shape mods of the face-turning
cube, as evidenced by their axes of rotation.
Neglecting the trivial apex turns, this
octahedron is equivalent to a 3x3 cube without corners, but with the face
centres marked to show their orientations. This works just like the Pyraminx, but now there are parities
involved, since a turn creates edge 4-cycles.
Fig 27: (1) The elementary
commutator cycles three edges. (2) R U R' U R U2 R' cycles 3 edges. (3) R' U R
U' R' U2 R U R' U' R U2 swaps 2 edge pairs. (4) R' U F' U' F U' R U or R D' F
D2 F' D R' D2 flips 2 corners.
To solve:
1. Position
and rotate the tips and the corners so the colours match the corners.
2. Position
the edges using R U R' U R U2 R' to cycle three edges RU -> BU -> LU
-> RU
and/or
R' U R U' R' U2 R U R' U' R U2, to swap two pairs of edge pieces UF <->
UL & UR <-> UB.
3.
To flip RU & FU edges and restore parity, use
R' U F' U' F U' R U or R D' F D2 F' D R' D2.
There are 12 edges with 2 orientations each
(12!/2 * 2^11) and 6 fixed corners with 4 orientations each (1 * 4^6), The
total number is thus (12!/2 * 2^11)
*(1 * 4^6) = 2.009 * 10^15.
4x4
Trabjer’s Octahedron
Trabjer’s Octahedron fig 28(A) omits the trivial
rotations at each apex, and displaces the cuts so they enclose a triangular
centre. These pieces correspond to the corners of the
underlying 3x3 Cube, except that their orientation is not visible, so end up
with a 3x3 shape mod where the corners have no orientation, but the centers do.
In the 4x4 version, there is an additional cut
through each of the octahedral edge planes, so that each entire face can turn
making a 4x4 cut as in (B). (C) shows a heritage
6x6 version. This is a shape mod of the 4x4 cube but the solution needs to be
done differently for two reasons. Firstly, there are multiple solutions with no
preferred colour arrangements because whole faces can be arbitrarily permuted
and secondly, the three apex pieces of each colour, which correspond to the
cube face centres, are indistinguishable leading to parity violations and the
colours don’t define which face the pieces should be on.
In fig 28 (1-4) are shown the chosen starting
arrangement of the faces and the three elementary commutators corresponding to
those of the 4x4 cube in fig 10 which have the same periodicities. (5-7) show
the three derived commutators:
(a) F
r F' l' F r' F' l with inverse F' l' F r F' l F r'
(b) F
R F' L' F R' F' L with inverse F' L' F R F' L f R'
(c) F
r F' L' F r' F' L with inverse F' l' F R F' l F R'
Fig 28: (A) Trabjer’s octahedron, B the 4x4 version, C a 6x6 version.
(1) Solved arrangement U, R and D views. (2) F R F’ R’ flips two pairs of
triangular centres and cycles 3 edges.
(3) F r F’ r’ gives a 5 cycle each of edges and apex pieces. (4) f r f’
r’ induces two 3 cycles of apex pieces. (5) F
r F' l' F r' F' l cycles 3 apex pieces. (6) F R F' L' F R' F' L cycles
3 triangular centres. (7) F r F' L' F r' F' L cycles 3 edges.
Compare with fig 10 for the same algorithms on the 4x4 cube.
As can be seen these
3-cycle apex pieces, triangular centres and edges on the U faces and can be
used as the basis of an efficient solution, which works by proceeding from apex
pieces to centres to edges as follows:
1. Pick
an apex with four distinct colours or place four together if there are none.
2. Place
the other four remaining colours at the opposing apex.
3. Use
elementary moves, to place the remaining apex pieces switch pair out of the way
to avoid scrambling and existing set, culminating with the apex 3-cycle to
resolve any that are flipped by arranging a 3-cycle in which two of the pieces
have the same colour. At this point we can freely rearrange the face colours by
rotating whole faces without scrambling the apex pieces.
4. Use
the centre 3-cycle algorithm to place the triangular centres.
5. If
we come to the end and have an odd permutation of triangular centres, we have a
parity violation. Hence we make a face rotation to restore the triangular
centres to an even permutation (since a single rotation is an odd 4-cycle
permutation). This will rotate the four apex pieces, reversing their parity but
these can be restored by using a series of apex 3-cycles involving 2 pieces of
the same colour to induce swaps of two apex pieces in terms of visible colour
until they are all in the correct position. We can now perform a last 3-cycle
to place the final centres.
6. Now
use the edge 3-cycle algorithm to position the edges, using a 3-cycle with two
of the same colour if we end up needing to swap two.
 Evil
Eye Rhombic Dodecahedron
Evil
Eye Rhombic Dodecahedron
The “evil eye”, so called because some versions
have coloured centre pieces recessed at the edge centres, introduces yet further
variations to the theme. Again the axes of rotation are the same as the cube
and the rhombic dodecahedron is a form of cube in which the faces are elevated
into pyramids.
There are five layers, two face layers two
lateral slices and one centre slice as in a 5x5 cube, however, here the face
moves all commute with one another because their pieces do not intersect, but
the lateral slice moves scramble 8 faces. The eyeless evil eye shown consists
only of ‘edge’ and ‘corner’ pieces. The edges occur in pairs of a given colour.
We name the rotations as in a 5x5 cube.
 Fig
29: (1) Two views of the solved ‘evil eye’ puzzle looking down on the U and F
faces for comparison with the following moves. (2) r U r' U r U2 r' permutes
corners in a 5 cycle. (3) F' r U' r' F moves an edge between adjacent faces. (4) r U2 r' U r U' r' U2 r U' r' moves an edge between faces (5) r U r' U' r' F
r2 U' r' U' r U r' F' swaps two edges and two corners. (6) r U r' U r U2 r' U2
r U r' U r U2 r' U2
Fig
29: (1) Two views of the solved ‘evil eye’ puzzle looking down on the U and F
faces for comparison with the following moves. (2) r U r' U r U2 r' permutes
corners in a 5 cycle. (3) F' r U' r' F moves an edge between adjacent faces. (4) r U2 r' U r U' r' U2 r U' r' moves an edge between faces (5) r U r' U' r' F
r2 U' r' U' r U r' F' swaps two edges and two corners. (6) r U r' U r U2 r' U2
r U r' U r U2 r' U2
The sketch solution is as follows:
1. Position
the ‘eyes’ correctly in relation to the corner colours if the puzzle has them.
This can be done by making rotations involving the slice moves and at the end,
using f2 u' l r' f2 l' r u' f2 to 3-cycle the last 3.
2. The
puzzle can then be solved up to the centre slice by elementary moves.
Algorithms are then needed as in fig 29 (2) to (4) to move pieces into position
without single slice moves re-scrambling the puzzle.
3. The
final face can be aligned using a combination of the moves in fig 29 (5) and
(6).
4. If
a parity error arises due to two identical edge pieces remaining swapped, a
single edge from an identical pair can be moved using (3) or (4) and the
remaining scrambled elements resolved.
There are 24 corners and 24 edges, both of whose permutations
are even, and the edges are in indistinguishable pairs so the total number of
positions is 23!*24!/2^2/2^12 = 9.789* 10^41.
A tutorial solution is available here.
D The Skewb Series
The Skewb series presents
a cube whose rotational axes are on the corners but whose cuts are deep enough
to affect all 6 faces symmetrically. The original Skewb
(fig 2) had a single central cut slicing the cube faces into a diamond with
four triangular corners. The master version has two cuts and is analogous to
the 3x3 cube and the Elite version with three cuts is both analogous to the 4x4
cube with two large face moves and two narrow slice moves. The Elite thus has
the moves of both the original Skewb and the Master Skewb, so can perform all three solutions.
However, from here things differ from the 4x4
cube, because the edge wings and face pieces of the Elite Skewb
can only be placed by moves involving global commutators and the face pieces
come in 3 incompatible types, so commutators have to be found to cycle each of
the piece types in a non-scrambling sequence. The solution is made all the more
challenging because every move involves all 6 cube faces, requiring a lot of 3D
observation. We will investigate firstly the original skewb,
then the master and finally how to reduce the elite to the master version.
 Fig 30: (1) The elite skewb scrambled as an original skewb. (2) the white corners are correctly positioned. (3) The faces are now all correctly positioned, but the upper corners need to be reoriented. (4) The elite skewb scrambled as a master skewb. (5) The white edge complexes and corners are correctly positioned. (6) All edge complexes have been correctly positioned, working from the white face to the middle and then the top. Corners have moved but retain parity. (7) The centres and half of the faces are now correctly positioned using the commutators. (8) All faces are correct but the corners need to be swapped in pairs and reoriented.
Fig 30: (1) The elite skewb scrambled as an original skewb. (2) the white corners are correctly positioned. (3) The faces are now all correctly positioned, but the upper corners need to be reoriented. (4) The elite skewb scrambled as a master skewb. (5) The white edge complexes and corners are correctly positioned. (6) All edge complexes have been correctly positioned, working from the white face to the middle and then the top. Corners have moved but retain parity. (7) The centres and half of the faces are now correctly positioned using the commutators. (8) All faces are correct but the corners need to be swapped in pairs and reoriented.
Skewbs are based on a tetrahedral set of rotations on four corners of tetrahedral symmetry in the cube. The Skewb is thus closely related to the Pyraminx, forming an effective shape mod where the six edge pieces of the pyraminx correspond to the 6 square faces of the Skewb, and the four corner pieces (without the tips) correspond to four of the corners of the Skewb, in tetrahedral configuration, with the opposing tetrad of skewb corners being locked in opposing configuration.
Solving
the Original Skewb
A simple solution for the original skewb runs as follows. We use the notation R a clockwise rotation
about the ufr corner and L a clockwise rotation about ufl:
1. By
making elementary upper corner rotations, position each of the corners of the
first face (say white as bottom face) into correct position, so that the corner
colours on a given face match. This also correctly orders the colours of the
side faces. If a corner is incorrectly oriented when placed move it to the top
to one side or the other and rotate about it, taking any existing corners which
would be displaced out of the way and returning them after correctly placing
the new one. If you are on the last corner and when moved into DFR it needs to
be rotated clockwise, do an R move to take it to the UFL and rotate about it by
a clockwise skewb move. Conversely do an R’ move
taking it to UBR and rotate anticlockwise move. Then the other corner displaced
should return correctly as well.
2. The
algorithm R’ L R L’ will then swap the U and F centres and the L and R centres.
Use this to sequentially move the U colour to F on the face with the same lower
corner colours. Repeating if you appear to end up a single swapped pair until
all the centres are correct.
3. The
upper corners will now be correctly placed as they lie opposite to the
correctly placed lower corners. To re-orient them correctly apply (R’ L R L’)^2
which rotates the front two corners clockwise and back two anticlockwise. This
may need to be done twice if two of the corners are correct, to get all the
corners to consist of two pairs each way.
Solving
the Master Skewb
We use the notation ufr = R, ufl = L, dfl = D, ubl = U. The technique depends of first arranging the
corners with the correct orientation and one set of edge complexes in place on
the first layer to set the overall parity of the corners correctly and then to
use entirely commutators of one sort or another to arrange the remaining edges
centres and faces. These may change the rotations of the upper corners but they
will retain parity and can be corrected at the end.
1. Use
corner rotations to place the four edge complexes onto the first face (say
white) in the correct colour order in relation to their corners. Place a piece
to be inserted below one already positioned with white facing sideways. Do an upper rotation to bring the placed piece down then a lower
rotation to pair it to the one to be inserted and return.
2. Use
upper rotations to place and orient the upper corners correctly. Correctly
rotate each by moving up and rotating. Then move this piece back down and
restore a neighbouring lower corner by an inverse move if it was displaced by
the upper rotation.
From now on all
moves have to be some sort of commutator aba'b'
to preserve the parity of the corners, but corners are now allowed to
move because commutators preserve corner parity.
3. Place second
level edge complexes, by moving each complex out by a before doing b' then a' carries the edge complex back into
position and b moves it up: a b' a'
b. To move across a face move the
piece first and take it on and undo both. To an adjacent edge take out of the way move the other
then move back and on. One can move around the sides and opposite (top) face to get them all int position without rescrambling any.
4. Align top layer
edge complexes by permuting UL>UR>UF>UL by R' L R L'.
5. Cycle centres
F>U>L>F by R U' R' U This will also move faces and corners.
6. Swap FUL and FDR
faces using a = R U' R' U D' U D U'.
To swap face pieces between adjacent or opposing faces, apply r a
r' where r is a rotation from a neighbouring side (or two rotations from
both neighbouring sides to swap between opposing faces), as in fig 31(4).
7. Swap and rotate opposing
pairs of corners (UFL <> UBR. and DBL <> DFR)
using b = (R U' R' U)^3 (or equivalently (U' R
U R')^3 ).
You can use r b
r' where r rotates the closer (UFL) corner to the same top colour as the
further corner (UBR).
8. Rotate corners
DBL antic and DFR clock by (U' R U R')^3,
(U R' U' R)3.
The Bearded Cubing tutorial
used for my solution. Jaap’s solution
page.
Fig 31: (1) Scrambled Elite
(2) The three skewb cuts showing the 2 slice moves
and two large face moves. (3) Elementary commutators permuting the Elite edges
and faces in a way which can reduce it to a Master Skewb.
(4) the green face and white centre (upper image) are folded to the left using a
lower move and then a commutator to swap diametrical pairs in a cube face.
Reducing
the Elite to the Master Skewb
We use the notation ufr(1, 2) = R(1, 2), ufl(1, 2) =
L(1, 2), dfl(1, 2) = D(1, 2), ubl(1,
2) = U(1, 2) where R is the Elite/Master face turn, R1 is the first slice, and
R2 the second (equivalent to the inverse of the first slice of the opposing
corner rotation).
The commutators below provide a sequence of moves
which can rearrange the smaller pieces into groups forming the edge and faces
of the Master Skewb shown in 31 (4, 5):
1. R1
L1’ R1’ L1 cycles small square faces in 2 3-cycle sets as shown in fig 31(3a).
2. R1
L2’ R1’ L2 cycles small edge wings in 2 3-cycle sets as shown in fig 31(3b).
The mirror formulae e.g. R2 L1 swap the complementary edge wings.
3. L1
U’ L1’ U cycles 3 inner faces and 5 outer faces as well as pieces permuted by
1, 2 above.
4. L2
U’ L2’ U cycles 3 outer faces and 5 inner faces as well as pieces permuted by
1, 2 above.
The strategy thus consists of (a) using 3, 4 and
their variants to group inner and outer faces together and then using 1, 2 and
their variants to correctly place the small faces and edge wings together to
form the Master edge complexes. These permutations can also be combined with setup moves where a piece is ported on a slice move and the 3-cycle is performed followed by the inverse setup to place arbitrary pieces into their correct position.
Antonio Vivaldi’s tutorial on the Elite Skewb, and solving the Master Skewb.
For the standard Skewb,
there are 4 fixed corners with 3 orientations each, 4 free corners with 3
orientations each and 6 face pieces giving a maximum of 6!*4!*38 positions.
This limit is not reached because, the total twist of the corners is fixed (3),
the faces must have an even permutation (2), the free corners must have an even
permutation, and hence form a tetrad (2), finally because the tetrads are
distinct the orientations one tetrad and the position of one of the others
corners will determine the positions of the other three (3). This leaves
6!*4!*3^6/4 = 3,149,280 positions.
For the Master version again because
the corner rotations move corners across face diagonals, the corner orbits
consist of two corner tetrads which never intermingle. Similarly, the
off-centre face pieces fall into two orbits - corresponding to the two corner
tetrads. There are 8 corners with 3 orientations each, 6 face centre pieces,
two sets of 12 other face pieces, and 12 edge pieces which (like the dino cube) cannot be flipped. This gives a maximum of
4!*3^8*6!*12!^3 positions.
Again this limit is not reached
because: The total twist of the corners is fixed (3). The faces centres must
have an even permutation (2). The edges must have an even permutation (2). The
free corners must have an even permutation, and hence form a tetrad (2). The
orientations of the fixed corners and the position of one of the free corners
will determine the positions of the other three (3). 12 face pieces in each
orbit come in six identical pairs (2!^12)
This gives a total of 4!*3^8*6!*12!^3/(2^15*3^2)
= 4.225*10^28 positions.
For the Elite version there are now 2
sets of 12 edge wings with no flips in 2 orbits, 2 sets of 12 small faces in
indistinguishable pairs, 2 sets of 12 outer faces, and 2 sets of 12 inner faces
again in pairs:
This gives a total of 4!*3^8*6!*12!^10/(2^41*3^2)
= 3.643*10^81 positions.
D: Edge turning puzzles
There are a series of puzzles in which rotations
occur on axis symmetries protruding from the edges of a give geometrical
polyhedron. These include the Cubic Curvy Copter, Skewby
Copter Twins fig 2 (23,8), the tetrahedral Mastermorphix
(18), and other variants such as the MF8 Helicopter dodecahedron fig 32. These
share a two-tiered structure of moves, where the primary (non-jumbling) moves
are 180o rotations of an edge. While the edge pieces now have fixed
positions, this results in a set of face orbits which are braided into a number
of separate strands, as shown 2 in fig 32 for the Curvy Copter and Mastermorphix. Complementing these, there are jumbling
moves shown 1 in fig 232, in which pairs of edge-turning assemblies can in turn
have two face pairs swapped thus making a double exchange between the braided
orbits. In the case of the cubes the corner orbits are still fully entangled (a
corner can end up in any corner position) but in the Mastermorphix
the non-jumbling corner moves form two tetrads, as they are transformationally
equivalent to the 3x3 cube under 180o rotations.
The Mastermorphix was
first made by several producers in 2009, four years after the helicopter cube.
Intriguingly the solution of the Mastermorphix as a
jumbling edge-turning puzzle equates to reducing the full 3x3 cube group to the
subgroup G3 of 180o rotations, precisely the last
subgroup in Thistlethwaite’s algorithm. Thus not only
is the Mastermorphix a dual between the cubic
rotational geometry of the axis cuts and the overall tetrahedral geometry of
the puzzle, but the edge-turning, jumbling solution is identical to the group
reduction method for the cube.
Due to the braided face orbits the non-jumbling
solutions are relatively easy to perform without the need for brute force
algorithms, while the jumbling states can also be unwound by exchanging pairs
of faces which are out of orbit.
Fig 32: (1) Both
the Mastermorphix and all forms of helicopter puzzle
enable jumbling moves, the former by making a 90o half-turn and the
latter by a turn of about 71o on two faces, as shown. (2) Without
jumbling, both puzzles have braided edge orbits that become entangled only when
the jumbling moves are taken into account, where two pairs of pieces are
exchanged between distinct orbits. The corner
orbits are two tetrads in the former and a cuboidal entangled orbit in the
latter. (3) Both the Mastermorphix and the
plus series of copter cubes such as the Skewby-copter
plus and twins (illustrated) can exchange corner pieces and centre faces. (4) The MF8 Helicopter dodecahedron.. (5) Evolution of helicopter design from helicopter through curvy copter, copter plus, 2x2, to Skewby plus and Twins which doesn't cut like a 2x2 but enables additional skewb edge splits..
A
sketch non-jumbling solution for the Curvy Copter is as follows, where F
R B L, are 180o rotations on the top layer. See in RedKB’s
non-jumbling
and jumbling
tutorials:
1. Orient
all the edge pieces on the first (initially top) face to their correct colours.
2. Flip
one edge down and use the distinct orbits and non-jumbling edge rotations to
move the top (say red) edge pieces onto the two face positions on the side
flipped face and flip up to the top. Repeat so the top face is complete.
3. Corner-edge
trios
(a) Find correct corner
to match top layer, flip it to the bottom and if necessary swing the corner around
the bottom (4 steps) to orient it (by four 1/3 rotations) so that a single side
edge flip will place it in the top layer in the correct orientation.
(b) Move correctly
coloured faces in the orbit of each adjacent face to adjacent and flip up into
position, taking the corner out of the way for the second adjacent move and
flip and flip the trio to the top. This completes the top half of the side
faces.
(c) Now flip the cube
over and use the unsolved top layer to hold pairs of side faces and flip to the
appropriate side layer keeping the edge orientations correct. This will
automatically leave the top faces correctly as they are the left-over pieces in
the raided orbits.
4. Finalize Corners
(a) Permute top face corners in a 3-cycle
holding ULF fixed using R L B L B R B L B L.
(b) Orient 3 corners
holding ULF fixed using (F R B L)^6
anticlockwise or (L B R F)^6 clockwise.
Additional jumbled solution moves:
(a) If
a triangle is out of orbit, swap with an adjacent top face colour by flipping
both to opposite sides and jumbling.
(b) To
flip an edge and swap two adjacent corners fig 33(a), use JR JL F, where JR is
jumbling with 2 clockwise twists JL anticlockwise twists.
Fig 33: (a) Flip an edge
and adjacent corners, (b,c) swapping out of orbit faces.
(c) Using R L JR F R L, swap two pairs Y,
G (starred and locked in the same orbit fig 33(b) and the red triangles
(starred and in neighbouring orbits, but of the same colour), these initially
swapped in the R L to be opposite.
(d) Use the same move
(fig 3(c)) to escape an orbit trap (the yellow and red ones, thumb and index
finger in the same orbit and the two red starred ones). Use F R F R to 3-cycle faces
(yellow, red as shown and green on top).
The Curvy Copter can also enter
jumbled non-cubic states, which need to be solved beforehand.
Fig 34: The skewby copter plus has almost unlimited potential to
combine, copter, jumbling, mixing and skewb moves in
succession, resulting in highly scrambled states, mixing and flipping all
possible pieces: (1) a partial rotation followed by a copter flip (single
jumble) is then followed by undoing the first move (2). A flip of the top back
edge in (2) then gives two opposite “ears” whose centers
can then be swapped (3) a mixing move, as in the curvy copter plus. However
this still permits a skewb move (4) which again
allows further scrambled copter and mixing moves (5). (6) A single mixing move
from (1) allows exchange of a corner and a centre, which can then move the
corner back to a centre position (7, 8) and we can see both exchanged in (9).
(10) shows a skewb move followed by two irregular
jumbling moves in succession.
However, the Skewby
Copter Plus and Twins present a far more formidable challenge. Firstly, there
are mixing as well as jumbling moves, in which multiple partial edge rotations
can both exchange centres and corners (3 in fig 32) and virtually all
successive jumbling moves can be performed with non-cubic piece colliding. The skewb moves also separate the arts of the edge complexes
causing these to become scrambled. In addition Skewb
moves further scramble the non-cubic conformation, requiring re-association of
inverted and rotated face sections.
Fig 35: Skewby
Copter Plus scrambled and partially-solved in a cubic state. The twins version
The solution involves first reducing the jumbled
puzzle to the cube. Much of the early phase is intuitive, but involves using skewb moves with commutator-type cancellations, as well as
unjumbling moves. Some of the above types of moves also apply, for example
re-pairing corners with their ‘ears’ using an inverse of the move in fig 32(3)
and taking a rotated centre mixed by the move in fig 32(3) in four step of edge
moves around a side to re-orient it before unmixing
it again. The second phase is edge
reduction to reunite the pieces of the edge complexes which have been mixed by
the skewb moves. Then the face pieces need to be
reduced before we have a final curvy copter solution.
The only way to come anywhere close to
understanding a full solution is to follow Antonio Vivaldi, who has a suite of
tutorials both, scrambling
and solving the skewby copter plus in three stages: making the cube, edge reduction, face reduction and endgame.
Here is a summary of the methods using only the
basic skewb commutator and curvy copteralgorithms
and very careful inspection and cancellation of scramblings,
generating compound commutators on the fly:
To regain cubic
shape from a completely scrambled state:
1. Combine skewb
moves and copter edge rotations to reposition flipped edge pieces within the
copter face wings to match flips.
2. Combine skewb
moves and partial copter rotations to pair large and small edge pieces in the
wings.
3. Do copter rotations and
jumbling moves to resolve ear formations in pairs, using a half skewb move if we find a formation that has no pair.
4. Reorient
centre pieces by putting them in corner position as in fig 34(1) and passing
them around 4 or 5 sides before returning them.
Now
reduce to curvy copter plus and then curvy copter.
1. Pair edge complex wings using
a skewb move. Position the edge complex centres using
a skewb commutator - e.g. ld
rd lu ru
to 3-cycle edge complex faces e.g. Ul > Fd > Df. Then do an edge
rotation and reverse the commutator rd ld ru lu.
If the skewb move separates existing edge complex centers, skewb + copter rotation
+ unskewb. To avoid damaging existing edge complexes
displace affected pieces by skewb moves which are
reversed after completion. This gets more complicated as we solve more out.
2. Position and orient corners
taking them round a square edge to reorient as with the curvy copter solution.
3. If one corner remains
incorrectly oriented, there is a parity violation. This needs to be solved by a
skewb move rotating this corner which will also move
three adjacent corners and disrupt existing edge complexes. These can be
restored by combining a skewb + a copter turn + an unskewb.
4. Match colours of face pieces
from the same orbit using double-jumbling if necessary and skewb
moves to place small and large centres of the same colour together unskewbing afterwards to keep parity and edge complexes.
Ideally position two pairs so they are solved together by the skewb move.
5. To reposition centres in
pairs use jumble moves to put each opposite and do a mixing flip to swap the
two before undoing the jumble moves. Curvy copter plus moves.
6. Finish using curvy copter
moves.
To estimate the number of positions on the copter series of cubes, we first
consider the helicopter cube, without jumbling moves (only 180o
rotations). Any permutation of the corners is possible, including odd
permutations. Seven of the corners can be independently rotated, and the
orientation of the eighth depends on the other seven, giving 8!_3^7
combinations. There are 24 face centres, which can be arranged in 24! different
ways. But the face centres actually occur in 4 distinct orbits, each containing
all colours. So the number of permutations is reduced to 6!^4 arrangements. The permutation of the face centres is
even, the number of permutations is divided by 2. Assuming the cube does not
have a fixed orientation in space, and that the permutations resulting from
rotating the cube without twisting it are considered identical, the number of
permutations is reduced by a factor of 24, because all 24 possible positions
and orientations of the first corner are equivalent because of the lack of
fixed centres. This gives a total
number of permutations of 7!*3^6*6!^4/2 = 4.936*10^17.
When a Helicopter Cube is scrambled with jumbling
moves but still retains its cube shape, then face centers
do not occur in 4 distinct orbits. Assuming that the four centres of each
colour are indistinguishable, the number of permutations is reduced to
24!/(4!^6) arrangements, because there are 4! ways to arrange the four pieces
of each of 6 colours. This gives a total number of permutations of
7!*3^6*24!/4!^6= 1.192*10^22.
For the curvy copter with 12 edges with fixed
positions these figures become:
Non-jumbling: 7!*3^6*6!^4*2^12*24/2 = 4.853*10^22.
Jumbling: 7!*3^6*24!/4!^6*2^12*24 = 1.172*10^27.
Fig 36: Non-cubic positions
on the helicopter cube. Order: the
size of the symmetry group. Index of the symmetry group as a subgroup of the
full cubic group (48 divided by the order). This is also the number of ways any
particular shape with that symmetry can be oriented in space (including
reflections). Shapes: the number of shapes found for each symmetry group not
counting mirror images. Mirror image counts the mirror image shapes. Total is Index
* Mirror image.
To count non-cube positions, we need to count all
possible shapes (ignoring the colours) , which is tricky, since sometimes moves
are blocked purely due to the shape of the pieces rather than the underlying
mechanism, although not for the skewby+. An analysis
by Matt Galla found 14,098 shapes, or 28,055 if
mirror images are counted too. Some of these have symmetry however, and
therefore occur in fewer than 24 (or 48) possible orientations. Multiplying
this with the previous result gives 1.529 * 10^33 for the curvy copter.
For the curvy copter plus, allowing exchanges
between corner and centre faces for the plus version would give a further 32!/4!^6
variations, giving a total of 2.105*10^60.
For the Skewby Copter
Plus, we have 5 faces types each indistinguishable in 4’s of the same colour,
the edges are now with two wings so 2^12 becomes 24! We still have non cubic
positions and corners exchanged with edges as above. The 24 centres have 3
orientations. The value would be something like 7!*3^6*(24!/4!^6)^5*24!*24*1.305*10^6*3^24*32!/4!^6
= 1.002*10^154.

Fig 37: MF8 Windows Grilles (1) Corner moves, (2) Scrambled, (3) Centres
reduced and edge wings aligned.
E: Interacting Face and Corner
Rotations: Windows Grilles and Crazy Unicorn
These two puzzles provide further examples where
there are interacting orbits of differing types, in these cases involving both
3x3 cube face moves and dino corner moves and in the
case of the crazy unicorn additional centre moves which link the corner and
edge moves in constrained orbits which preserve the relationship between pairs
of centre pieces. In both these puzzles the reduced scrambling results in
solutions where the corner moves tends to resolve themselves as braided orbits
come together as the last few pieces become resolved. Like the NxN cubes, we proceed by reduction to a 3x3 solution.
On the windows grilles,
let’s define the small clockwise corner rotation by FRU and the large by fru. We proceed by first completing the centre squares,
then aligning the edge complexes, first by pairing the edge wings to either
side of the centre, then the lateral wings rotated by the smaller corner moves
and finally the centre pieces, before moving on to the next edge assembly. These can be done using moves which
don’t re-scramble edge assemblies by taking critical pieces out of the way of a
given corner rotation and then at the end using a commutator on the centre
pieces.
A
sketch reduction is as follows:
1.
Complete the centre squares by face moves and
then larger corner moves to fold the correct centre triangles into place. If
you get two triangles to swap on the last 2 faces, use a neighbouring complete
face to bring in one triangle and swap it in the second move to reverse the 3
cycle colours.
2. We
now align the edge assemblies,
consisting of 2 edge corners, 2 wings and a center
without disturbing the centre triangles. With a give left edge wing in UF, use
FRU' U L' FRU ( L U') to move the right wing from adjacent to the FUR corner. Like
the 4x4 and 5x5 cubes, face moves will not upset edge assembly alignments. Bring
them together, without disruption, by first rotating the second edge wing in
using fru’ moving the edge assembly out of the way by
face moves and then undoing the fru to relocate the
centre triangles in the above commutator.
3. To
align the corner edges e.g. the right, move it to adjacent to the FUR corner,
along with 2 other unaligned edge corners and twist using face moves to
position it with the correct flip to rotate in correctly.
4. To
align a center from UR to UF, apply FRU' FLU FRU
FLU'. Make sure it is flipped correctly to rotate into position.
This will completely
align the edge assemblies one by one, leaving 3 at the end to align together.
5. To
align the last three edge wing pairs, arrange remaining edge sets UL, UF and UR,
check a clockwise rotation of flu will align the UF pair and apply R' flu U' R
U flu' R'.
6. Align
the last corner edges by moving 3 bad ones to the flu corner in sequence
and swapping the three corner edges until all are aligned, by applying R' fru' R bru.
7. Cycle
the three centres UR -> UF -> UL via FRU' FLU FRU FLU'. If two centres
are flipped you will need to do a face move to position them so that a corner
rotation can flip them.
8. To
rotate the single fru corner clockwise, apply (R BRU
R' FRU)^2. For anticlockwise, reverse the corner moves. In some solution approaches,
it is also possible to get 2-edges centres swapped although it doesn’t appear
here.
RubikArt
has a very good tutorial
on this solved intuitively. It is in Spanish, but you can arrange YouTube to
provide real-time subtitles in English and several other languages, by
selecting the settings cog wheel, choosing subtitles and re-entering to select
automatic translation. See in particular: 3.33 centres, 7.32 edges, 13.24 last
3 edges, 18.19 last corner edges, 19.26 3x3 solve, 22.21 last corner.
The number of moves,
calculated by multiplying the 3x3 configuration by the the edge piece
configurations and additional corner orientations is:
4.325*10^19*24!^3/4!^6*2^(24*3+12)*3 = 3.137*10^108.
Crazy Unicorn
The
crazy unicorn introduces three different kinds of rotations, 3x3 face moves,
corner rotations on only a single tetrad of corners (hence the unicorn) and
crazy moves in the centre, where only face rotations of adjacent faces move the
centre pieces, but rotation of their own face leaves them fixed, as shown for
the blue piece in fig 38(1).
This
confines the centre piece orbits.
Only the triangles and larger wedge centres are moved by corner
rotations. The triangles are moved only by corner rotations, and thus have
confined separate orbits. The smaller wedge pieces are confined to rotate
within their adjacent face as a fixed set of four. The larger wedges are
subject to both rotations and face moves of their adjacent face rotations and
these preserve pairs of wedges, which move together in sequences of these two
moves following identical orbits. In addition, corner moves can take place only
if there are a net set of 180o rotations of the faces, otherwise
they are prevented from turning by the inverted edge sections (1, 2). These
constraints make the puzzle in Antonio Vivaldi’s words “a puzzle within a
puzzle”.
Fig 38: (1) The state after
an anticlockwise front corner rotation followed by a 90o U, showing
the face move has not shifted the centre pieces in the U layer. (2) A scrambled
cube. (3) Centre resolved into squares with the correct triangle pieces. (4)
Centre pieces fully reduced. (5) Edges aligned ready for a 3x3 solve.
We
use a strategy of reduction in which the centre triangles are first trivially
aligned with their centres (1), to complete the squares fig 38(3). We then have
to rotate the faces until all the corner moves are accessible by 3x3 face moves
including edge flips. We can then use commutator-like moves (3) to orbit the
larger centre wedge pairs into their correct centre. The last sets of pairs
will all rationalize by applying one of the moves in (3). We then pair the
edges (4), using commutator-like moves to avoid scrambling existing edge pairs.
One then does a modified 3x3 solve (5, 6, 7) to ensure the centres end up in
the correct positions:
(1) Orient centre
triangles using corner moves
(2) Set non corner
centres in position
(3) Use triangle moves
such as
(a) F2 flu+ frd+ F2 flu- frd- to move pairs
of rotating centres into position
(b) flu- frb-
U2 flu+ frb+ U2 to exchange 4 on the same level
avoiding
disturbing existing pieces
(4) Pair the edges using e.g. for large
piece G in fu using F2 flu- T F2 flu+ T'
where
T' moves the small complement g of G into fd,
avoiding breaking good pairs.
(5) Make a white cross
taking an edge aside e.g. to ld, before flipping the
white centres down using F2 to
join the edge to
the centres with D and take them up with F2.
(6) Place the corners and
middle edges as on a 3x3.
(7) Use F R U R' U' F' to
permute the edges to match one centre and then repeatedly to permute the
remaining edges
holding uf fixed until all match. You may need to
flip some edges here.
(8) Perform the usual
corner cycles and rotations to complete (R U R' U' F', R U R' U R U2 R',
U R U' L' U R' U' L,
(R' D' R D)^4).
Pete’s tutorial used for
my solution is here.
Antonio’s tutorial is here.
E:
Puzzles with Irregular Scrambled Conformations: Square-1, Sun Cube and Cool Flying Swallow.
Square-1
Fig 39: Square-1 solved,
scrambled in cubic shape and two non-cubic arrangements.
Square-1 is a cubic
puzzle with top and bottom faces consisting of four corners and four edges with
the edges having half the angle of the corners, separated by a middle layer
with a single cut that enables ‘half’ the pieces at a time constitution a 180o
slice to be switched between top and bottom. Because the corners have twice the
angle, these moves can result in a number of different geometries, with
differing numbers of available slice twists, from 4 top and bottom in the cubic
state down to one or two in other states. The non-cubic states comprise a
variety of forms, including states with broken symmetry which can be accessed
through different slices through the centre move of the odd permutation (fig
40). Some of these can be exited at only a few positions.
If we view the cube from
the right hand face and define:
– = flip right half
through centre section
t/b = rotate top/bottom
clockwise one feasible cut line
op(k) = op^k op = move sequence
Repeated operations have
some very long orbits.
(a) {(t–)(82)
}visits many non-cubic states before returning to the cube. The full
periodicity back to the completed cube is 4*82 = 328 since the permutation of
the corners (1 - 8) and the edges (a-h) is (1728)(ag)(cd).
(b) {(tb–)(8)} returns to the cube permuted by (148)(263)(57)(afbecgdh) requiring period 3*8*8 = 192.
Fig 40: Non-cubic cascade
of positions and a sample of cubic solution algorithms I originally used to
solve Square-1.
The solution consists of first reducing the
puzzle to cubic form using the upper sequence of moves in fig 40. Elementary
rotations followed by algorithms such as op1-10 shown in fig 40 then complete the
solution.
To swap top and bottom op0={t-t(4)b(4)-t(-1)}.
To calculate the number of moves for the Square-1,
there are three categories of puzzle shapes. Both layers have 4 edges and 4
corners each. One layer has 3 corners, 6 edges, the other 5 corners 2 edges.
One layer has 2 corners, 8 edges, the other 6 corners and no edges. There are
1, 3, 10, 10 and 5 layer shapes with 6, 5, 4, 3 and 2 corners. This means there
are 5*1+10*3+10*10+3*10+1*5 = 170 shapes for the top and bottom layers. The
middle layer has two shapes (half of it is assumed to be fixed). This means
that there seem to be 170*2*8!*8! = 552,738,816,000 positions if we disregard
rotations of the layers. Some layer shapes however have symmetry, and these
have been counted too many times this way.
To take account of the symmetries we can simply
count the number of layer shapes differently. Instead of the numbers 1, 3, 10,
10, 5 we use the numbers 2, 36, 105, 112, 54, which are the number of shapes if
we consider rotations different (e.g. a square counts as 3 because it has three
possible orientations). By the same method as before we then get 19305*2*8!*8!
or 62,768,369,664,000 positions. To exclude layer rotations, divide by 12^2 to
get a total of 15!/3 = 435,891,456,000 distinct positions.
If instead we wish to count only all those
positions where there are no corner pieces in the way of twisting the halves,
then we can use the same method but counting only all the different ways each
shape can be split into two halves, e.g. a square counts as 2 this time. The
numbers to plug in are now 1, 12, 46, 62, and 37 which gives a total of
3678*2*8!*8! = 1.196*10^13 twistable
positions.
Sun
Cube
The MF8 Sun Cube and its closely equivalent
cousin, the DaYan Bagua
cube, extend the rotations of the 3x3 cube by providing cuts and additional
pieces which also permit face rotations in steps of 45o. This splits
the edge and centre pieces, resulting in 4 pairs of left- and right-handed kite
face pieces and 8 small wedge face pieces on each face of the cube. The 45o
rotations when combined on successive faces in sequence can also rapidly lead
to non-cubic geometries which become bandaged, either externally, by splits
which prevent rotation, or left and right handed kites which internally prevent
a further rotation because their internal structures are mirror images of one
another, although several 45o rotations can cause them to become
exchanged.
Fig
41: (1) A sun pattern on the sun cube generated by repeated applications of F+
B- R2 L2 U2 D2 F- B+ R2 L2 U2 D2 F2 B2. (2) Scrambled by a sequence of 45o
moves. (7) Fully scrambled stickerless version. (3)
All corners on the front face by 45o twists and 180o flips. (4) The
commutator F+ R F- R’ cycles 3 small wedges and 5 kites. (6) (F+ R F- R’)^9
returns to the cubic shape cycling 5 kites. (6) The algorithm U+
Li U- 2F Li U L 2F U+ L U- cycles three small wedges and also makes 3x3 moves. (8)
The algorithm 2R U+2R D- 2R U+ 2R U- 2R U- D+ Ri
cycles and unbandages three wedges, leaving a swapped
corner and edge (9), which can be swapped by using Ri
Di R D repeatedly. Right decomposition. Even the corners decompose into three sub-pieces.
Define M+ as a clockwise 45o rotation
of face M and M- the inverse with M and M’ being the usual 90o
rotations.
We sketch a solution based on Dan Avi's tutorial below, in the following stages:
(1)
Reduce to the cubic shape. Try to get a single square face. To flip an edge put
it in a corner position and apply Ri
Di R D repeatedly until flipped. Do the same thing to swap and edge and a
corner.
(2)
Unbandage the edge kites (12.38). Needs edge pieces on unbandaged
DR DB and R, B faces of UR UB to apply the algorithm 2R
U+2R D- 2R U+ 2R U- 2R U- D+ Ri which 3-cycles kites
around the UB edge, as shown 8 in fig 41.
This leaves the cube with a corner and edge on the top and bottom
swapped, so repeat Ri Di R D to regain the cube
shape.
(3)
Reduce the centres (21.17).
Three
cycle small triangles completing the centre square, using U+ Li U- 2F Li U L 2F
U+ L U-.
(4)
Reduce the edges (45.21). This can be done
intuitively by looking for matchable edge slices and using top and bottom 45o
turns and a 180o flip to align, using commutator like moves to keep aligned
small centre wedges unscrambled to bring together misaligned kites. Join the
wedges take the aligned edge out of the way and then reverse the alignment move
to restore the centre wedges before restoring the edge assembly.
(5)
3x3 solve.
(6) Fix parity if
necessary, resolve and complete. To swap 2 corners UFL and
UFR apply U+ 2R U- Di 2F U+. Then swap the protruding corner and edge pieces
top and bottom using Ri Di R D repeatedly. This may
result in having to do (2) (3) and (4) over again to fix some scrambled pieces,
before a final 3x3 solve.
Dan Avi’s scrambling
the sun cube and tutorial
and parity fix.
An approximate estimate of the
number of cubic configurations of the sun cube, counting the kite face pieces
of a given colour as indistinguishable is: 4.325*10^19 *(48!/(8!^6))^2 / 2 =
1.805*10^86.
Son-Mum
Cube
The Son-Mum, or son mother cube is in a sense a complement
of the sun cube, because it allows centre slice moves to make 45o turns, which still enable face rotations as shown in Evolution of the
son-mum is similar to that of the curvy copter. The original expanded by adding
additional slant cuts in the edge pieces permitting additional 45o turns which enable the puzzle to enter more disordered states. A 4x4 version of
the original was then developed enabling the original to commute with
additional 4x4 permutations. Finally in the 4x4 v2 both
of these effects are combined as in (3) in fig 41b.
Fig 41b: (1) Evolution of
the son-mum. (2) The puzzle permits reversed parity. (3) Sequence of moves
leading to separation of edges and wedges. (4) Son-mum v2 from fully scrambled
to solved. See 1 and 2, 3 for original solution.
The rotations are made possible by the centre pieces descending into
the interior at 45o to the surface, thus enabling the rotations in 3
(a, b, c) to take place. The position in (c) still enables all the 3x3 face
moves to take place resulting in further scrambled states. These rotations can
cause the protruding edge pieces to become rotated and for the outer small
faces to become flipped as in (d). If edge pieces are moved into faces with the
flipped edge centres and rotated, as in (e) the small edge centre pieces are now
aligned in a way which allows the R move, which has just begun to separate the
edge piece front right from its small corner slice, enabling a turn, which enters
a new set of more highly scrambled states.
The required moves, where [ ]+/- are 45o moves about the
z-axis of the whole puzzle are:
[U+ D-]- R L' U' D
R' L'
[U- D+]- sloping U edge F
R L' U' D' R' L
[U+ D-]- taking us to (d)
[U+ D-]-+ into
fluted face
F R B L all edges
horizontal
[U- D+] arriving at (e).
In (4 a, b) are two highly scrambled states which eventually become locked. One has a severely flipped small corner face and the next shows two edge wedges flipped and separated from their edge. The solution proceeds as follows. First the puzzle needs to be unlocked by finding moves which release others, so we can make more than one rotation. We then need to match the edges with their correct wedges. This makes it possible to bring the puzzle back into the subset of states permitted in the original son-mum version (c) and then to cubic form (d) . Moves in and out of diagonal states (e) can then be used to reduce the puzzle to a 3x3 Rubik and solved (f). In the case of the 4x4 we will end up with that solution.
For the standard Son-mum cube Antonio Vivaldi has solutions 1 & 2 and Dan Avi has one.
Cool
Flying Swallow
The Dayan Shuang Fei Yan, or Cool Flying
Swallow cube has no face turns but instead four sets of three oblique face
turns set in tripets around one of the tetrahedral
corner tetrads, and a set of four dino corner
rotations, with a slightly different curvature, intersecting the oblique
rotations on the complementary tetrad.
Fig 42: (1) An oblique face
rotation left and a corner rotation right. (2) The oblique FLU corner algorithm
U' R U R' L R' L' R L' U L U' rotates a corner and associated edge wings and
the lower edge by 120o. Both intersecting oblique rotations (3) can and oblique
and corner rotations combined (4) can translocate pieces across the cube. (5)
Stages in QBando's solution in order of piece type.
(6) Bon Bon's algorithms have non-cubic intermediates (see right). (7) A corner
rotation can simultaneously interact with three oblique rotations to induce
global changes. (8) An oblique FLU commutator (U' R U R')^6 induces a 6-cycle,
in which a corner and adjacent edge pieces are rotated and cycled in each (U' R
U R')^2 step.
This presents a radically different situation to that
found in the Sun or Skewby Copter where the non-cubic
conformations tend to be obstructed and increasingly confined in their
rotations and the final algorithms are performed in the cubic state. Instead it
is the non-cubic states which provide the riches repertoire of algorithms.
With the exception of the forbidden move
combinations trying to mix moves with conflicting curvature, all the other move
combinations result in transformations which can rapidly carry pieces in orbits
all over the cube surface leading to a plethora of highly-scrambled non-cubic
states.
QBAndo
has a tutorial solving the cube, which is in
Spanish, but can be viewed using English subtitles by adjusting the settings as
in the Windows Grilles tutorial. A shorter explanation of the movements in
English can be found here.
A suite
of nine algorithm examples are also provided by Bon Bon: 0 1 2 3 4 5 6 7 8.
Because
of the highly irregular conformations, it is difficult to give a precise
account of the method of solution. QBAndo’s method is
a form of reduction positioning the pieces in order of their type rather than
face by face. To estimate the number of cubic
positions, we have 4 fixed corners with 3 rotations and 4 floating corners with
3 rotations, 12 fixed oblique centres, 12 edges which can’t be flipped in their
cubic positions, 12 triangular centres in indistinguishable pairs, 6
rectangular centres, 12 edge wings and 12 each of LH and RH quadrilateral faces
each in indistinguishable pairs, giving as a first rough approximation
3^4*4!*3^4*12!*12!/2^12*6!*12!*(12!/2^12)^2 = 4.160*10^40 positions, assuming
the oblique rotations allow odd permutations.
However,
this is a significant underestimate of the total positions, because the
interesting transformations arise from non-cubic positions and haven’t been
counted. If we consider the non-cubic positions it appears that the floating
corners, edges and triangular centres all count as 40 mixable corners with 3
orientations and the rectangular centres edge wings and quadrilateral centres
all count as 42 mixable edges with 2 flips and the oblique centers
have potentially 5 orientations corresponding to the available cuts. Hence a
total estimate comes to 5^12*3^4*40!*3^40/2^12*42!*2^42/2^24 =
1.764*10^130.
The
size of the order of magnitude difference is due to most of the scrambling
having to take place in non-cubic positions in which there is no bandaging.
References
Demaine et al. (2011)
Algorithms for Solving Rubik’s Cubes arXiv: 1106.5736 [cs.DS]
El-Sourani
N Hauke S, Borschbach M
(2010) An Evolutionary Approach for Solving the Rubik’s Cube Incorporating
Exact Methods C.
In Di Chio et al. (Eds.): EvoApplications 2010, Part I, LNCS 6024 80–89.
Kaur H (2015) Algorithms for
solving the Rubik's cube A study of how to solve the Rubik’s cube using two
popular approaches: the Thistlewaite’s algorithm and
the IDA* algorithm.
http://www.diva-portal.org/smash/get/diva2:816583/FULLTEXT01.pdf
Korf R (1997) Finding optimal
solutions to Rubik's cube using pattern databases. AAAI/IAAI Jul 27 700-705.
Kunkle, D., & Cooperman, G. (2007,
July). Twenty-six moves suffice for Rubik's cube. In Proceedings of the 2007
international symposium on Symbolic and algebraic computation (pp. 235-242).
ACM.
Nelson R (2018) Abstracting the
Rubik’s Cube, Math Horizons, 25/4 18-22.
Rokicki, T. (2008). Twenty-five moves
suffice for Rubik's cube. arXiv preprint
arXiv:0803.3435.
Rokicki, T. (2010). Twenty-Two Moves
Suffice for Rubik’s Cube®. The Mathematical Intelligencer, 32(1), 33-40.
Rokicki, T., Kociemba,
H., Davidson, M., & Dethridge, J. (2014). The
diameter of the rubik's cube group is twenty. SIAM
Review, 56(4), 645-670.doi:10.1137/140973499.
van Grol,
R 2010 The Quest for God's Number Math Horizons 18/2
doi:10.4169/194762110X535961.